数列{an}中,a1=1,且点(an,an+1)在直线l:2x-y+1=0上.
(Ⅰ)设bn=an+1,求证:{bn}是等比数列;
(Ⅱ)设Cn=n(3an+2),求{Cn}的前n项和.
解:(Ⅰ)数列{a
n}中,a
1=1,且点(a
n,a
n+1)在直线l:2x-y+1=0上.
所以2a
n-a
n+1+1=0,即2a
n+2=a
n+1+1,
所以{a
n+1}是以2为首项,2为公比的等比数列,
所以a
n+1=2×2
n-1=2
n,
a
n=2
n-1,
b
n=a
n+1=2
n,
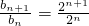
=2
所以{b
n}是等比数列;
(Ⅱ)设C
n=n(3a
n+2)=3n×2
n-n,
{C
n}的前n项和.
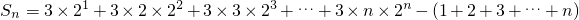
,
令T=3×2
1+3×2×2
2+3×3×2
3+…+3×n×2
n,…①,
所以2T=3×2
2+3×2×2
3+3×3×2
4+…+3×n×2
n+1…②,
①-②得:-T=3(2
1+2
2+2
3+…+2
n-n×2
n+1),
T=3(n-1)•2
n+1+6,
所以

.
分析:(Ⅰ)利用已知条件得到{a
n+1}是以2为首项,2为公比的等比数列,求出a
n,通过b
n=a
n+1,利用等比数列的定义证明{b
n}是等比数列;
(Ⅱ)求出C
n=n(3a
n+2),利用错位相减法求出3×2
1+3×2×2
2+3×3×2
3+…+3×n×2
n的和,然后求出{C
n}的前n项和.
点评:本题考查数列的递推关系式,通项公式的求法,前n项和的求法,错位相减法的应用,考查计算能力,转化思想的应用.

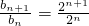 =2
=2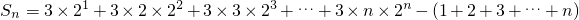 ,
, .
.
