
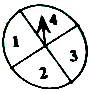
 ��Ӣ����ijһ���ֽ�Ŀ�У���һ�ֹ�����Ϸ���������£�ת��ͼ��ת�̣�һ��Բ���ĵȷ֣���ÿ�������ڷֱ��������1��2��3��4������ת��ֹͣʱָ����ָ���־����Ƿ���أ��ڴ�n��ʱ��תn�Σ�����ת������֮�ʹ���n2ʱ���㴳�سɹ������������أ�����ֹͣ���أ�������һ���ܻ��10ŷԪ��֮��ÿ�ളһ�أ�����������ÿ�������߶���������ص����ܹ���Ϊֹ������ת��ÿ��ת������������
��Ӣ����ijһ���ֽ�Ŀ�У���һ�ֹ�����Ϸ���������£�ת��ͼ��ת�̣�һ��Բ���ĵȷ֣���ÿ�������ڷֱ��������1��2��3��4������ת��ֹͣʱָ����ָ���־����Ƿ���أ��ڴ�n��ʱ��תn�Σ�����ת������֮�ʹ���n2ʱ���㴳�سɹ������������أ�����ֹͣ���أ�������һ���ܻ��10ŷԪ��֮��ÿ�ളһ�أ�����������ÿ�������߶���������ص����ܹ���Ϊֹ������ת��ÿ��ת���������������� ��1���ǡ�ij�˲μ�һ����Ϸ��ǡ�û��10ŷԪ��Ϊ�¼�A��
��������ֻ�����˵�һ�أ�û�й��ڶ��أ��ɴ��������ĸ��ʣ�
��2����������֪X�����п���ȡֵ�������Ӧ�ĸ��ʣ�
д���������X�ĸ��ʷֲ���������ѧ����ֵ��
��� �⣺��1���ǡ�ij�˲μ�һ����Ϸ��ǡ�û��10ŷԪ��Ϊ�¼�A��
������֪����ֻ�����˵�һ�أ�û�й��ڶ��أ�
��ˣ�����һ��ת����2��3��4�е�һ����
�ڶ���ת���ˣ�1��1������1��2������1��3������2��1������2��2���е�һ����
������ĸ���ΪP��A��=$\frac{3}{4}$����5��$\frac{1}{16}$��=$\frac{15}{64}$��
��2���������⣬X�����п���ȡֵΪ0��10��20��40��
����P��X=0��=$\frac{1}{4}$��P��X=10��=$\frac{15}{64}$��
P��X=20��=$\frac{3}{4}$��$\frac{11}{16}$��$\frac{54}{64}$=$\frac{891}{2048}$��
P��X=40��=$\frac{3}{4}$��$\frac{11}{16}$��$\frac{10}{64}$=$\frac{165}{2048}$��
��X�ĸ��ʷֲ�Ϊ��
| X | 0 | 10 | 20 | 40 |
| P | $\frac{1}{4}$ | $\frac{15}{64}$ | $\frac{891}{2048}$ | $\frac{165}{2048}$ |
���� ���⿼������ɢ����������ķֲ�������ѧ�����ļ������⣬���е��⣮


 ��ʱѵ���������������ϵ�д�
��ʱѵ���������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | 5 | C�� | 7 | D�� | 9 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com