
分析 (Ⅰ)由4a=8,即$2×\frac{1}{2}×2c×b=2\sqrt{3}$,b2+c2=4,即可求得b和c的值,由$e<\frac{{\sqrt{2}}}{2}$.即可求得$b=\sqrt{3}$,c=1,即可椭圆的方程;
(Ⅱ)分类讨论:当y0=0时,即可求得x0=±2,即可求得直线与曲线的交点;
当y0≠0时,则直线l的方程为$y=\frac{{12-3{x_0}x}}{{4{y_0}}}$,代入椭圆方程,由点P(x0,y0)为曲线C上一点,解得x=x0,代入直线方程,y=y0,故直线l与曲线C有且有一个交点P.
解答 解:(Ⅰ)依题意,设椭圆C的方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,焦距为2c,
由题设条件知,4a=8,a=2,$2×\frac{1}{2}×2c×b=2\sqrt{3}$,b2+c2=a2=4,
所以$b=\sqrt{3}$,c=1,或b=1,$c=\sqrt{3}$(经检验不合题意舍去),
故椭圆C的方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$.
(Ⅱ)证明:当y0=0时,由$\frac{{{x_0}^2}}{4}+\frac{{{y_0}^2}}{3}=1$,可得x0=±2,
当x0=2,y0=0时,直线l的方程为x=2,直线l与曲线C有且只有一个交点(2,0).
当x0=-2,y0=0时,直线l的方程为x=-2,直线l与曲线C有且只有一个交点(-2,0).
当y0≠0时,直线l的方程为$y=\frac{{12-3{x_0}x}}{{4{y_0}}}$,联立方程组$\left\{\begin{array}{l}y=\frac{{12-3{x_0}x}}{{4{y_0}}}\\ \frac{x^2}{4}+\frac{y^2}{3}=1.\end{array}\right.$,
消去y,得$(4{y_0}^2+3{x_0}^2){x^2}-24{x_0}x+48-16{y_0}^2=0$.①
由点P(x0,y0)为曲线C上一点,得$\frac{{{x_0}^2}}{4}+\frac{{{y_0}^2}}{3}=1$,可得$4{y_0}^2+3{x_0}^2=12$.
于是方程①可以化简为${x^2}-2{x_0}x+{x_0}^2=0$,解得x=x0,
将x=x0代入方程$y=\frac{{12-3{x_0}x}}{{4{y_0}}}$可得y=y0,故直线l与曲线C有且有一个交点P(x0,y0),
综上,直线l与曲线C有且只有一个交点,且交点为P(x0,y0).
点评 本题考查椭圆的标准方程及简单几何性质,直线与椭圆的位置关系,考查分类讨论思想,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{{2\sqrt{14}}}{9}$ | B. | $\frac{{\sqrt{14}}}{9}$ | C. | $\frac{{\sqrt{11}}}{5}$ | D. | $\frac{{2\sqrt{11}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 | 8日 | 9日 | 10日 | 11日 | 12日 | 13日 | 14日 | 15日 |
| AQI指数 | 72 | 74 | 115 | 192 | 138 | 123 | 74 | 80 | 105 | 73 | 91 | 90 | 77 | 109 | 124 |
| PM2.5 | 36 | 29 | 76 | 112 | 89 | 85 | 40 | 32 | 59 | 35 | 45 | 59 | 53 | 79 | 89 |
| PM10 | 76 | 86 | 148 | 199 | 158 | 147 | 70 | 83 | 121 | 75 | 96 | 90 | 63 | 113 | 140 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(1)+f(3)<2f(2) | B. | f(1)+f(3)≤2f(2) | C. | f(1)+f(3)>2f(2) | D. | f(1)+f(3)≥2f(2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
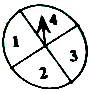 在英国的某一娱乐节目中,有一种过关游戏,规则如下:转动图中转盘(一个圆盘四等分,在每块区域内分别标有数字1,2,3,4),由转盘停止时指针所指数字决定是否过关.在闯n关时,转n次,当次转得数字之和大于n2时,算闯关成功,并继续闯关,否则停止闯关,闯过第一关能获得10欧元,之后每多闯一关,奖金翻倍.假设每个参与者都会持续闯关到不能过关为止,并且转盘每次转出结果相互独立.
在英国的某一娱乐节目中,有一种过关游戏,规则如下:转动图中转盘(一个圆盘四等分,在每块区域内分别标有数字1,2,3,4),由转盘停止时指针所指数字决定是否过关.在闯n关时,转n次,当次转得数字之和大于n2时,算闯关成功,并继续闯关,否则停止闯关,闯过第一关能获得10欧元,之后每多闯一关,奖金翻倍.假设每个参与者都会持续闯关到不能过关为止,并且转盘每次转出结果相互独立.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$ | B. | $\frac{3π}{4}$ | C. | π | D. | $\frac{3π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com