
分析 (I)f(0)=0,f′(x)=ex+e-x.f′(0)=2.利用点斜式即可得出切线方程.
(II)令g(x)=ex-e-x-k(x+$\frac{{x}^{3}}{6}$),g(0)=0.g′(x)=ex+e-x-k(1+$\frac{1}{2}{x}^{2}$).x∈(0,1),
①k≤0时,g′(x)≥0,函数g(x)在x∈(0,1)上单调递增,g(x)>g(0)恒成立.
②当k>0时,g″(x)=ex-e-x-kx=h(x).g″(0)=0.h′(x)=ex+e-x-k,h′(0)=2-k.
(i)当0<k≤2时,h′(x)>h′(0)=2-k≥0.函数g″(x)在x∈(0,1)上单调递增,可得g″(x)>0.进而达到函数g(x)在x∈(0,1)上单调递增,满足条件.
(ii)e+e-1≥k>2时,h′(0)=2-k<0,h′(1)=e+e-1-k>0,可得函数h′(x)存在零点x0∈(0,1),h′(x0)=${e}^{{x}_{0}}+{e}^{-{x}_{0}}$-k=0.利用导数研究其单调性可得:函数g(x)在在(0,x0)上单调递减,因此g(x)<g(0),不符合题意,舍去.
(iii)k>e+e-1,h′(1)=e+e-1-k<0,函数g″(x)在x∈(0,1)上单调递增,g″(x)<0.可得函数g(x)在x∈(0,1)上单调递减,g(x)<g(0)=0恒成立.舍去.
解答 解:(I)f(0)=0,f′(x)=ex+e-x.∴f′(0)=2.
∴曲线y=f(x)在点(0,f(0))处的切线方程为y-0=2(x-0),可得2x-y=0.
(II)令g(x)=ex-e-x-k(x+$\frac{{x}^{3}}{6}$),g(0)=0.
g′(x)=ex+e-x-k(1+$\frac{1}{2}{x}^{2}$).
∵x∈(0,1),∴①k≤0时,g′(x)≥0,函数g(x)在x∈(0,1)上单调递增,g(x)>g(0)恒成立.
②当k>0时,g″(x)=ex-e-x-kx=h(x).g″(0)=0.
h′(x)=ex+e-x-k,h′(0)=2-k.
(i)当0<k≤2时,h′(x)>h′(0)=2-k≥0.函数g″(x)在x∈(0,1)上单调递增,∴g″(x)>0.
可得g′(x)在x∈(0,1)上单调递增,可得:g′(x)>g′(0)=2-k≥0,函数g(x)在x∈(0,1)上单调递增,g(x)>g(0)恒成立.
(ii)e+e-1≥k>2时,h′(0)=2-k<0,h′(1)=e+e-1-k>0,∴函数h′(x)存在零点x0∈(0,1),h′(x0)=${e}^{{x}_{0}}+{e}^{-{x}_{0}}$-k=0.函数h(x)在(0,x0)上单调递减;在(x0,1)上单调递增.h(0)=g″(0)=0.h(x)min=h(x0)=${e}^{{x}_{0}}$-${e}^{-{x}_{0}}-k{x}_{0}$<g″(0)=0.∴函数g′(x)在(0,x0)上单调递减,g′(x)<g′(0)=2-k<0,可得函数g(x)在在(0,x0)上单调递减,因此g(x)<g(0),不符合题意,舍去.
(iii)k>e+e-1,h′(1)=e+e-1-k<0,函数g″(x)在x∈(0,1)上单调递增,∴g″(x)<0.可得g′(x)在x∈(0,1)上单调递减,可得:g′(x)<g′(0)=2-k<0,函数g(x)在x∈(0,1)上单调递减,g(x)<g(0)=0恒成立.舍去.
综上可得:实数k的最大值为2.
点评 本题考查了利用导数研究函数的单调性极值与最值、方程与不等式的解法、分类讨论方法、等价转化方法、分析法、函数零点存在定理,考查了推理能力与计算能力,属于难题.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案科目:高中数学 来源: 题型:选择题
| A. | cosx•sinx | B. | cos2x+sin2x | C. | 2cosx•sinx | D. | cos2x-sin2x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(1)+f(3)<2f(2) | B. | f(1)+f(3)≤2f(2) | C. | f(1)+f(3)>2f(2) | D. | f(1)+f(3)≥2f(2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
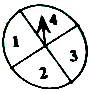 在英国的某一娱乐节目中,有一种过关游戏,规则如下:转动图中转盘(一个圆盘四等分,在每块区域内分别标有数字1,2,3,4),由转盘停止时指针所指数字决定是否过关.在闯n关时,转n次,当次转得数字之和大于n2时,算闯关成功,并继续闯关,否则停止闯关,闯过第一关能获得10欧元,之后每多闯一关,奖金翻倍.假设每个参与者都会持续闯关到不能过关为止,并且转盘每次转出结果相互独立.
在英国的某一娱乐节目中,有一种过关游戏,规则如下:转动图中转盘(一个圆盘四等分,在每块区域内分别标有数字1,2,3,4),由转盘停止时指针所指数字决定是否过关.在闯n关时,转n次,当次转得数字之和大于n2时,算闯关成功,并继续闯关,否则停止闯关,闯过第一关能获得10欧元,之后每多闯一关,奖金翻倍.假设每个参与者都会持续闯关到不能过关为止,并且转盘每次转出结果相互独立.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$ | B. | $\frac{3π}{4}$ | C. | π | D. | $\frac{3π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | a>c>b | C. | c>b>a | D. | b>a>c |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com