
【题目】已知函数![]() ,
,![]() .
.
(1)设函数![]() (
(![]() ),讨论
),讨论![]() 的极值点个数;
的极值点个数;
(2)设直线![]() 为函数
为函数![]() 的图像上一点
的图像上一点![]() 处的切线,试探究:在区间
处的切线,试探究:在区间![]() 上是否存在唯一的
上是否存在唯一的![]() ,使得直线
,使得直线![]() 与曲线
与曲线![]() 相切.
相切.
【答案】(1)当![]() 时,
时,![]() 有两个极值点,
有两个极值点,![]() 时,
时,![]() 没有极值点.(2)存在,答案见解析
没有极值点.(2)存在,答案见解析
【解析】
(1)求出函数的导数![]() ,令
,令![]() ,根据
,根据![]() 的符号,分类讨论,即可求解;
的符号,分类讨论,即可求解;
(2)由![]() ,求得切线的方程
,求得切线的方程![]() ,设直线
,设直线![]() 与曲线
与曲线![]() 相切于点
相切于点![]() ,由
,由![]() ,说明
,说明![]() 的方程也是
的方程也是![]() ,再证明在区间
,再证明在区间![]() 上
上![]() 存在且唯一即可.
存在且唯一即可.
(1)由题意,函数![]() ,
,
可得![]() (
(![]() ),令
),令![]() .,
.,
①当![]() 即
即![]() 时,
时,![]() 在
在![]() 上恒成立,此时
上恒成立,此时![]() 在
在![]() 上单调递增,极值点个数为0
上单调递增,极值点个数为0
②当![]() 时,
时,![]() 在
在![]() 上恒成立,此时
上恒成立,此时![]() 在
在![]() 上单调递增,极值点个数为0;
上单调递增,极值点个数为0;
③当![]() 时,
时,![]() ,设
,设![]() ,
,![]() 是
是![]() 的两根,则
的两根,则![]() ,
,![]() ,故
,故![]() ,
,![]() ,此时
,此时![]() 在
在![]() 上有两个极值点.
上有两个极值点.
综上所述,当![]() 时,
时,![]() 有两个极值点,
有两个极值点,![]() 时,
时,![]() 没有极值点
没有极值点
(2)因为![]() ,可得
,可得![]() ,
,
所以切线![]() 的方程为
的方程为![]() ,即
,即![]()
设直线![]() 与曲线
与曲线![]() 相切于
相切于![]() ,∵
,∵![]() ,∴
,∴![]() 即
即![]() ,
,
∴![]() ,
,
∴直线![]() 的方程也为
的方程也为![]() ,即
,即![]() ,
,
∴![]() ,即
,即![]() .
.
下证:在区间![]() 上
上![]() 存在且唯一,设
存在且唯一,设![]() (
(![]() ),
),
![]() ,则在
,则在![]() 上单调递增.
上单调递增.
又![]() ,
,![]() ,
,
由零点存在性定理知:存在![]() ,使得
,使得![]() ,即
,即![]() .
.
故在区间![]() 上存在唯一的
上存在唯一的![]() ,使得直线
,使得直线![]() 与曲线
与曲线![]() 相切.
相切.


科目:高中数学 来源: 题型:
【题目】一批产品共10件,其中3件是不合格品,用下列两种不同方式从中随机抽取2件产品检验:
方法一:一次性随机抽取2件;
方法二:先随机抽取1件,放回后再随机抽取1件.
记方法一抽取的不合格产品数为![]() .记方法二抽取的不合格产品数为
.记方法二抽取的不合格产品数为![]() .
.
(1)求两种抽取方式下![]() ,
,![]() 的概率分布列;
的概率分布列;
(2)比较两种抽取方式抽到的不合格品平均数的大小?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以直角坐标系的原点
为参数),以直角坐标系的原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求圆![]() 的极坐标方程;
的极坐标方程;
(2)设曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,求三条曲线
,求三条曲线![]() ,
,![]() ,
,![]() 所围成图形的面积.
所围成图形的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的两个顶点A,B的坐标分别为(![]() ,0),(
,0),(![]() ,0),圆E是△ABC的内切圆,在边AC,BC,AB上的切点分别为P,Q,R,|CP|=2
,0),圆E是△ABC的内切圆,在边AC,BC,AB上的切点分别为P,Q,R,|CP|=2![]() ,动点C的轨迹为曲线G.
,动点C的轨迹为曲线G.
(1)求曲线G的方程;
(2)设直线l与曲线G交于M,N两点,点D在曲线G上,![]() 是坐标原点
是坐标原点![]() ,判断四边形OMDN的面积是否为定值?若为定值,求出该定值;如果不是,请说明理由.
,判断四边形OMDN的面积是否为定值?若为定值,求出该定值;如果不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,
,![]() 、
、![]() 为椭圆的左、右焦点,
为椭圆的左、右焦点,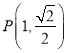 为椭圆上一点,且
为椭圆上一点,且![]() .
.
(1)求椭圆的标准方程;
(2)设直线![]() ,过点
,过点![]() 的直线交椭圆于
的直线交椭圆于![]() 、
、![]() 两点,线段
两点,线段![]() 的垂直平分线分别交直线
的垂直平分线分别交直线![]() 、直线
、直线![]() 于
于![]() 、
、![]() 两点,当
两点,当![]() 最小时,求直线
最小时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解户籍性别对生育二胎选择倾向的影响,某地从育龄人群中随机抽取了容量为![]() 的调查样本,其中城镇户籍与农民户籍各
的调查样本,其中城镇户籍与农民户籍各![]() 人;男性
人;男性![]() 人,女性
人,女性![]() 人.绘制不同群体中倾向选择生育二胎与倾向选择不生育二胎的人数比例图(如图所示),其中阴影部分表示倾向选择生育二胎的对应比例,则下列叙述中错误的是( )
人.绘制不同群体中倾向选择生育二胎与倾向选择不生育二胎的人数比例图(如图所示),其中阴影部分表示倾向选择生育二胎的对应比例,则下列叙述中错误的是( )
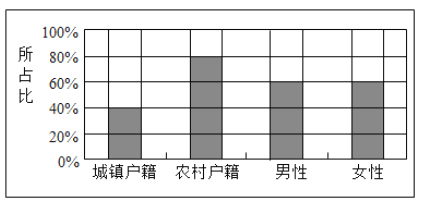
A.是否倾向选择生育二胎与户籍有关
B.是否倾向选择生育二胎与性别无关
C.倾向选择生育二胎的人员中,男性人数与女性人数相同
D.倾向选择不生育二胎的人员中,农村户籍人数少于城镇户籍人数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com