
【题目】已知△ABC的两个顶点A,B的坐标分别为(![]() ,0),(
,0),(![]() ,0),圆E是△ABC的内切圆,在边AC,BC,AB上的切点分别为P,Q,R,|CP|=2
,0),圆E是△ABC的内切圆,在边AC,BC,AB上的切点分别为P,Q,R,|CP|=2![]() ,动点C的轨迹为曲线G.
,动点C的轨迹为曲线G.
(1)求曲线G的方程;
(2)设直线l与曲线G交于M,N两点,点D在曲线G上,![]() 是坐标原点
是坐标原点![]() ,判断四边形OMDN的面积是否为定值?若为定值,求出该定值;如果不是,请说明理由.
,判断四边形OMDN的面积是否为定值?若为定值,求出该定值;如果不是,请说明理由.
【答案】(1)![]()
![]() .(2)四边形OMDN的面积是定值,其定值为
.(2)四边形OMDN的面积是定值,其定值为![]() .
.
【解析】
(1)根据三角形内切圆的性质证得![]() ,由此判断出
,由此判断出![]() 点的轨迹为椭圆,并由此求得曲线
点的轨迹为椭圆,并由此求得曲线![]() 的方程.
的方程.
(2)将直线![]() 的斜率分成不存在或存在两种情况,求出平行四边形
的斜率分成不存在或存在两种情况,求出平行四边形![]() 的面积,两种情况下四边形
的面积,两种情况下四边形![]() 的面积都为
的面积都为![]() ,由此证得四边形
,由此证得四边形![]() 的面积为定值.
的面积为定值.
(1)因为圆E为△ABC的内切圆,所以|CA|+|CB|=|CP|+|CQ|+|PA|+|QB|=2|CP|+|AR|+|BR|=2|CP|+|AB|=4>|AB|
所以点C的轨迹为以点A和点B为焦点的椭圆(点![]() 不在
不在![]() 轴上),
轴上),
所以c![]() ,a=2,b
,a=2,b![]() ,
,
所以曲线G的方程为![]()
![]() ,
,
(2)因为![]() ,故四边形
,故四边形![]() 为平行四边形.
为平行四边形.
当直线l的斜率不存在时,则四边形![]() 为为菱形,
为为菱形,
故直线MN的方程为x=﹣1或x=1,
此时可求得四边形OMDN的面积为![]() .
.
当直线l的斜率存在时,设直线l方程是y=kx+m,
代入到![]() ,得(1+2k2)x2+4kmx+2m2﹣4=0,
,得(1+2k2)x2+4kmx+2m2﹣4=0,
∴x1+x2![]() ,x1x2
,x1x2![]() ,△=8(4k2+2﹣m2)>0,
,△=8(4k2+2﹣m2)>0,
∴y1+y2=k(x1+x2)+2m![]() ,|MN|
,|MN|![]()
点O到直线MN的距离d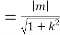 ,
,
由![]() ,得xD
,得xD![]() ,yD
,yD![]() ,
,
∵点D在曲线C上,所以将D点坐标代入椭圆方程得1+2k2=2m2,
由题意四边形OMDN为平行四边形,
∴OMDN的面积为S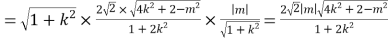 ,
,
由1+2k2=2m2得S![]() ,
,
故四边形OMDN的面积是定值,其定值为![]() .
.


科目:高中数学 来源: 题型:
【题目】某校从高一年级期末考试的学生中抽出60名学生,其成绩(均为整数)的频率分布直方图如图所示.

(1)估计这次考试的平均分;
(2)假设分数在[90,100]的学生的成绩都不相同,且都在94分以上,现用简单随机抽样方法,从95,76,97,88,69,100这6个数中任取2个数,求这2个数恰好是两个学生的成绩的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设关于![]() 的一元二次方程
的一元二次方程![]() .
.
(1)若![]() 是从
是从![]() 四个数中任取的一个数,
四个数中任取的一个数,![]() 是从
是从![]() 三个数中任取的一个数,求上述方程有两个不等实根的概率.
三个数中任取的一个数,求上述方程有两个不等实根的概率.
(2)若![]() 是从区间
是从区间![]() 任取的一个数,
任取的一个数,![]() 是从区间
是从区间![]() 任取的一个数,求上述方程有实根的概率.
任取的一个数,求上述方程有实根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)设函数![]() (
(![]() ),讨论
),讨论![]() 的极值点个数;
的极值点个数;
(2)设直线![]() 为函数
为函数![]() 的图像上一点
的图像上一点![]() 处的切线,试探究:在区间
处的切线,试探究:在区间![]() 上是否存在唯一的
上是否存在唯一的![]() ,使得直线
,使得直线![]() 与曲线
与曲线![]() 相切.
相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】西安市自2017年5月启动对“车不让人行为”处罚以来,斑马线前机动车抢行不文明行为得以根本改变,斑马线前礼让行人也成为了一张新的西安“名片”.
但作为交通重要参与者的行人,闯红灯通行却频有发生,带来了较大的交通安全隐患及机动车通畅率降低,交警部门在某十字路口根据以往的检测数据,得到行人闯红灯的概率约为0.4,并从穿越该路口的行人中随机抽取了200人进行调查,对是否存在闯红灯情况得到![]() 列联表如下:
列联表如下:
30岁以下 | 30岁以上 | 合计 | |
闯红灯 | 60 | ||
未闯红灯 | 80 | ||
合计 | 200 |
近期,为了整顿“行人闯红灯”这一不文明及项违法行为,交警部门在该十字路口试行了对闯红灯行人进行经济处罚,并从试行经济处罚后穿越该路口行人中随机抽取了200人进行调查,得到下表:
处罚金额 | 5 | 10 | 15 | 20 |
闯红灯的人数 | 50 | 40 | 20 | 0 |
将统计数据所得频率代替概率,完成下列问题.
(Ⅰ)将![]() 列联表填写完整(不需写出填写过程),并根据表中数据分析,在未试行对闯红灯行人进行经济处罚前,是否有99.9%的把握认为闯红灯与年龄有关;
列联表填写完整(不需写出填写过程),并根据表中数据分析,在未试行对闯红灯行人进行经济处罚前,是否有99.9%的把握认为闯红灯与年龄有关;
(Ⅱ)当处罚金额为10元时,行人闯红灯的概率会比不进行处罚降低多少;
(Ⅲ)结合调查结果,谈谈如何治理行人闯红灯现象.
参考公式:![]() ,其中
,其中![]()
参考数据:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.132 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
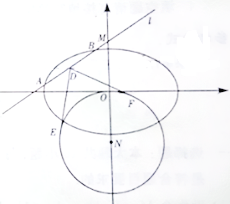
【题目】在平面直角坐标系xOy中,已知椭圆C: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,椭圆C截直线y=1所得线段的长度为
,椭圆C截直线y=1所得线段的长度为![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)动直线l:y=kx+m(m≠0)交椭圆C于A,B两点,交y轴于点M.点N是M关于O的对称点,⊙N的半径为|NO|. 设D为AB的中点,DE,DF与⊙N分别相切于点E,F,求![]() EDF的最小值.
EDF的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com