
【题目】已知椭圆![]() :
: ![]() (
(![]() )的离心率为
)的离心率为![]() ,
, ![]() 、
、![]() 分别是它的左、右焦点,且存在直线
分别是它的左、右焦点,且存在直线![]() ,使
,使![]() 、
、![]() 关于
关于![]() 的对称点恰好是圆
的对称点恰好是圆![]() :
: ![]()
![]() (
(![]() ,
, ![]() )的一条直径的两个端点.
)的一条直径的两个端点.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设直线![]() 与抛物线
与抛物线![]() (
(![]() )相交于
)相交于![]() 、
、![]() 两点,射线
两点,射线![]() 、
、![]() 与椭圆
与椭圆![]() 分别相交于点
分别相交于点![]() 、
、![]() .试探究:是否存在数集
.试探究:是否存在数集![]() ,当且仅当
,当且仅当![]() 时,总存在
时,总存在![]() ,使点
,使点![]() 在以线段
在以线段![]() 为直径的圆内?若存在,求出数集
为直径的圆内?若存在,求出数集![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
【答案】(Ⅰ)![]() ; (Ⅱ)见解析.
; (Ⅱ)见解析.
【解析】试题分析:(Ⅰ)椭圆的焦距![]() 等于圆
等于圆![]() 的直径,所以
的直径,所以![]() ,根据离心率求出
,根据离心率求出![]() ;
;
(Ⅱ)因为![]() 、
、![]() 关于
关于![]() 的对称点恰好是圆
的对称点恰好是圆![]() 的一条直径的两个端点,所以直线
的一条直径的两个端点,所以直线![]() 是线段
是线段![]() 的垂直平分线(
的垂直平分线(![]() 是坐标原点),故
是坐标原点),故![]() 方程为
方程为![]() ,与
,与![]() 联立得:
联立得: ![]() ,点
,点![]() 在以线段
在以线段![]() 为直径的圆内
为直径的圆内![]()
![]()
![]()
![]() 韦达定理代入求解即可.
韦达定理代入求解即可.
试题解析:
(Ⅰ)将圆![]() 的方程配方得:
的方程配方得: ![]() ,所以其圆心为
,所以其圆心为![]() ,半径为2.
,半径为2.
由题设知,椭圆的焦距![]() 等于圆
等于圆![]() 的直径,所以
的直径,所以![]() ,
,
又![]() ,所以
,所以![]() ,从而
,从而![]() ,故椭圆
,故椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)因为![]() 、
、![]() 关于
关于![]() 的对称点恰好是圆
的对称点恰好是圆![]() 的一条直径的两个端点,所以直线
的一条直径的两个端点,所以直线![]() 是线段
是线段![]() 的垂直平分线(
的垂直平分线(![]() 是坐标原点),故
是坐标原点),故![]() 方程为
方程为![]() ,与
,与![]() 联立得:
联立得: ![]() ,由其判别式
,由其判别式![]() 得
得![]() ,①
,①
设![]() ,
, ![]() ,则
,则![]() ,
, ![]() .
.
从而![]()
![]() ,
, 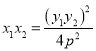
![]() .
.
因为![]() 的坐标为
的坐标为![]() ,所以
,所以![]() ,
, ![]() .
.
注意到![]() 与
与![]() 同向,
同向, ![]() 与
与![]() 同向,所以
同向,所以
点![]() 在以线段
在以线段![]() 为直径的圆内
为直径的圆内![]()
![]()
![]()
![]()
![]()
![]() ,②
,②
当且仅当![]()
![]() 即
即![]() 时,总存在
时,总存在![]() ,使②成立.
,使②成立.
又当![]() 时,由韦达定理知方程
时,由韦达定理知方程![]()
![]() 的两根均为正数,故使②成立的
的两根均为正数,故使②成立的![]() ,从而满足①.
,从而满足①.
故存在数集![]() ,当且仅当
,当且仅当![]() 时,总存在
时,总存在![]() ,使点
,使点![]() 在以线段
在以线段![]() 为直径的圆内.
为直径的圆内.


科目:高中数学 来源: 题型:
【题目】(本小题满分8分) 已知抛物线C:y=-x2+4x-3 .
(1)求抛物线C在点A(0,-3)和点B(3,0)处的切线的交点坐标;
(2)求抛物线C与它在点A和点B处的切线所围成的图形的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
①函数 ![]() 是奇函数;
是奇函数;
②存在实数x,使sinx+cosx=2;
③若α,β是第一象限角且α<β,则tanα<tanβ;
④ ![]() 是函数
是函数 ![]() 的一条对称轴;
的一条对称轴;
⑤函数 ![]() 的图象关于点
的图象关于点 ![]() 成中心对称.
成中心对称.
其中正确命题的序号为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】咖啡馆配制两种饮料,甲种饮料分别用奶粉![]() 、咖啡
、咖啡![]() 、糖
、糖![]() 。乙种饮料分别用奶粉
。乙种饮料分别用奶粉![]() 、咖啡
、咖啡![]() 、糖
、糖![]() 。已知每天使用原料限额为奶粉
。已知每天使用原料限额为奶粉![]() 、咖啡
、咖啡![]() 、糖
、糖![]() 。如果甲种饮料每杯能获利
。如果甲种饮料每杯能获利![]() 元,乙种饮料每杯能获利
元,乙种饮料每杯能获利![]() 元。每天在原料的使用限额内饮料能全部售出,每天应配制两种饮料各多少杯能获利最大?
元。每天在原料的使用限额内饮料能全部售出,每天应配制两种饮料各多少杯能获利最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列五个命题:①“若![]() ,则
,则![]() 或
或![]() ”是假命题;②从正方体的面对角线中任取两条作为一对,其中所成角为
”是假命题;②从正方体的面对角线中任取两条作为一对,其中所成角为![]() 的有48对;③“
的有48对;③“ ![]() ”是方程
”是方程![]() 表示焦点在
表示焦点在![]() 轴上的双曲线的充分不必要条件;④点
轴上的双曲线的充分不必要条件;④点![]() 是曲线
是曲线![]() (
(![]() ,
, ![]() )上的动点,且满足
)上的动点,且满足![]() ,则
,则![]() 的取值范围是
的取值范围是![]() ;⑤若随机变量
;⑤若随机变量![]() 服从正态分布
服从正态分布![]() ,且
,且![]() ,则
,则![]() .其中正确命题的序号是__________(请把正确命题的序号填在横线上).
.其中正确命题的序号是__________(请把正确命题的序号填在横线上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形OQRP为矩形,其中P,Q分别是函数f(x)= ![]() sinwx(A>0,w>0)图象上的一个最高点和最低点,O为坐标原点,R为图象与x轴的交点.
sinwx(A>0,w>0)图象上的一个最高点和最低点,O为坐标原点,R为图象与x轴的交点. 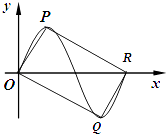
(1)求f(x)的解析式
(2)对于x∈[0,3],方程f2(x)﹣af(x)+1=0恒有四个不同的实数根,求实数a的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某货轮匀速行驶在相距![]() 海里的甲、乙两地间运输货物,运输成本由燃料费用和其他费用组成.已知该货轮每小时的燃料费用与其航行速度的平方成正比(比例系数为
海里的甲、乙两地间运输货物,运输成本由燃料费用和其他费用组成.已知该货轮每小时的燃料费用与其航行速度的平方成正比(比例系数为![]() ),其他费用为每小时
),其他费用为每小时![]() 元,且该货轮的最大航行速度为
元,且该货轮的最大航行速度为![]() 海里/小时.
海里/小时.
(1)请将从甲地到乙地的运输成本![]() (元)表示为航行速度
(元)表示为航行速度![]() (海里/小时)的函数;
(海里/小时)的函数;
(2)要使从甲地到乙地的运输成本最少,该货轮应以多大的航行速度行驶?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 的最小正周期为
的最小正周期为![]() .
.
(1)求![]() 的值;
的值;
(2)将函数![]() 的图像向左平移
的图像向左平移![]() 个单位,再将得到的图像上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数
个单位,再将得到的图像上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数![]() 的图像,求函数
的图像,求函数![]() 的单调递减区间.
的单调递减区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com