
分析 ①根据线性回归分析中相关系数的定义;②根据空间直角坐标系的坐标对称判断可知;③利用互斥事件的概念判断;④根据类比推理的概念判断;⑤由于点(x,y),(x′,y′)都在直线y=x上,得到参数的方程,直线y=3x上的点关于原点对称的点是原直线y=3x,同理可得参数的另一个方程,解方程组,求出参数的值,得到本题结论.
解答 解:对于①线性相关系数r的绝对值越接近于1,表明两个变量线性相关程度越强,③正确,
对于②空间直角坐标系中,(-2,1,9)关于x轴对称的点的坐标(-2,-1,-9);故②错.
对于③事件A:至少有一个命中,事件B:都命中,不是互斥事件;故③错
对于④由类比推理的定义知推理“半径为r圆的面积S=πr2,则单位圆的面S=π”不是类比推理;故④错.
对于⑤$|\begin{array}{l}{x'}\\{y'}\end{array}|=|\begin{array}{l}{2}&{-1}\\{p}&{q}\end{array}||\begin{array}{l}{x}\\{y}\end{array}|$
∴$\left\{\begin{array}{l}{x'=2x-y}\\{y'=px+qy}\end{array}\right.$.
∵点(x,y),(x′,y′)都在直线y=x上,
∴$\left\{\begin{array}{l}{x=y}\\{2x-y=px+qy}\end{array}\right.$,
∴p+q=1.
∵直线y=3x上的点关于原点对称的点是原直线y=3x,
∴点(x,y),(x′,y′)都在直线y=3x上,
∴$\left\{\begin{array}{l}{y=3x}\\{px+qy=3(2x-y)}\end{array}\right.$,
∴p+3q=-3.
∴q=-2,p=3.故⑤正确.
故答案为:①⑤
点评 本题考查相关系数,考查相关系数,考查直角坐标系的点的对称,考查互斥事件和类比推理的定义以及矩阵的变换,本题是一个综合题目.属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\sqrt{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{9}$ | B. | $-\frac{7}{9}$ | C. | $\frac{{4\sqrt{2}}}{9}$ | D. | $-\frac{{4\sqrt{2}}}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
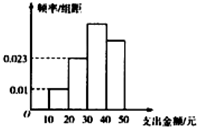 为了解学生在课外活动方面的支出情况,抽取了n个同学进行调查,结果显示这些学生的支出金额(单位:元)都在[10,50],其中支出金额在[30,50]的学生有134人,频率分布直方图如图所示,则n=( )
为了解学生在课外活动方面的支出情况,抽取了n个同学进行调查,结果显示这些学生的支出金额(单位:元)都在[10,50],其中支出金额在[30,50]的学生有134人,频率分布直方图如图所示,则n=( )| A. | 150 | B. | 160 | C. | 180 | D. | 200 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a1d>0 | B. | a1d<0 | C. | d>0 | D. | d<0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com