
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2016届安徽省高三第一次联考理科数学试卷(解析版) 题型:解答题
(本小题满分12分)
已知函数 ,其中
,其中 为正实数。
为正实数。
(1)当 时,求
时,求 在
在 上的零点个数。
上的零点个数。
(2)对于定义域内的任意 ,将
,将 的最大值记作
的最大值记作 ,求
,求 的表达式。
的表达式。
查看答案和解析>>
科目:高中数学 来源:2014-2015学年吉林省高二下学期期末理科数学试卷(解析版) 题型:解答题
已知函数 ,
, 在
在 时有极值,在
时有极值,在 处的切线方程为
处的切线方程为 .
.
(1)求a,b,c
(2)求 在
在 上的最大值.
上的最大值.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广西河池市高二下学期期末理科数学试卷(解析版) 题型:填空题
如图所示,在三棱锥S﹣ABC中,SA⊥SB,SB⊥SC,SC⊥SA,且SA,SB,SC和底面ABC所成的角分别为α1,α2,α3,△SBC,△SAC,△SAB的面积分别为S1,S2,S3,类比三角形中的正弦定理,给出空间图形的一个猜想是 .

查看答案和解析>>
科目:高中数学 来源:2016届重庆市高三10月月考文科数学试卷(解析版) 题型:选择题
已知函数f(x)=2mx3?3nx2+10(m>0)有且仅有两个不同的零点,则lg2m+lg2n的最小值为( )
A、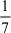 B、
B、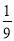 C、
C、 D、
D、
查看答案和解析>>
科目:高中数学 来源:2016届山东省高三上学期开学考试文科数学试卷(解析版) 题型:填空题
已知定义在 上的奇函数
上的奇函数 满足
满足 ,且
,且 时,
时, ,给出下列结论:
,给出下列结论:
① ;
;
②函数 在
在 上是减函数;
上是减函数;
③函数 关于直线
关于直线 对称;
对称;
④若 ,则关于
,则关于 的方程
的方程 在
在 上所有根之和为
上所有根之和为 .
.
其中正确的是 .(填上所有正确结论的序号)
查看答案和解析>>
科目:高中数学 来源:2016届山东省高三上学期开学考试理科数学试卷(解析版) 题型:选择题
下列推理过程是演绎推理的是
A.由平面三角形的性质推测空间三棱锥的性质
B.某校高二1班有55人,2班有52人,由此得高二所有班人数都超过50人
C.两条直线平行,同位角相等;若 与
与 是两条平行直线的同位角,则
是两条平行直线的同位角,则
D.在数列 中,
中, ,
, ,由此归纳出
,由此归纳出 的通项公式
的通项公式
查看答案和解析>>
科目:高中数学 来源:2016届江西省高三上学期第一次考试理科数学试卷(解析版) 题型:选择题
将函数 向右平移
向右平移 个单位,再将所得的函数图象上的各点纵 坐标不变,横坐标变为原来的
个单位,再将所得的函数图象上的各点纵 坐标不变,横坐标变为原来的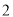 倍,得到函数
倍,得到函数 的图象,则函数
的图象,则函数 与
与 ,
, ,
, 轴围成的图形面积为( )
轴围成的图形面积为( )
A.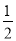 B.
B.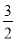 C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com