手拉手全优练考卷系列答案科目：高中数学 来源： 题型：解答题
（本小题满分14分）设函数
,
的两个极值点为
,线段
的中点为
.
(1) 如果函数为奇函数,求实数
的值;当
时，求函数图象的对称中心；
(2) 如果点在第四象限,求实数的范围;
(3) 证明:点也在函数的图象上,且为函数图象的对称中心.
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
（本题满分14分）
医学上为研究某种传染病传播过程中病毒细胞的发展规律及其预防，将病毒细胞注入一只小白鼠体内进行实验，经检测，病毒细胞在体内的总数与天数的关系记录如下表.已知该种病毒细胞在小白鼠体内的个数超过
的时候小白鼠将死亡.但注射某种药物，将可杀死此时其体内该病毒细胞的
.
(Ⅰ) 为了使小白鼠在实验过程中不死亡，第一次最迟应在何时注射该种药物?(精确到天)
（Ⅱ）第二次最迟应在何时注射该种药物，才能维持小白鼠的生命？(精确到天)
(参考数据：
，
)
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
（本小题满分12分）
已知函数f(x)=
（x∈R），Ｐ1（ｘ1，ｙ1），Ｐ2（ｘ2，ｙ2）是函数ｙ＝ｆ(x)图像上两点，且线段Ｐ1Ｐ2中点Ｐ的横坐标为
。
（１）求证Ｐ的纵坐标为定值； （4分）
（２）若数列｛
｝的通项公式为＝ｆ(
)(ｍ∈Ｎ
，ｎ＝１,２,３,…,ｍ），求数列｛｝的前ｍ项和
； （5分）
（３）若ｍ∈Ｎ时，不等式
＜
横成立，求实数a的取值范围。（3分）
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
（本题12分）已知集合
是同时满足下列两个性质的函数
组成的集合：
①在其定义域上是单调增函数或单调减函数；
②在的定义域内存在区间
，使得在上的值域是
．
(1)判断函数
是否属于集合？并说明理由．若是，则请求出区间；
(2)若函数
，求实数
的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
若函数f(x)是以2为周期的偶函数 ，且当x∈（0 ，1）时 ，
f(x) =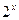 
－1 ．(1)求x∈（－1 ，1）时 f(x)的解析式 ；（2）求f(
)的值 ．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
(本题满分13分)
已知三次函数
的导函数
，
，
、
为实数。
（1）若曲线
在点（
，
）处切线的斜率为12，求的值；
（2）若在区间［-1，1］上的最小值、最大值分别为-2、1，且
，求函数的解析式。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
时，求函数
在
的值域；
的方程
有解，求
的取值范围
的最大值和最小正周期； 
三个内角，若，
，且C为锐角，求
的单调区间及极值