
已知函数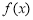 满足
满足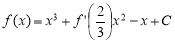 (其中
(其中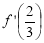 为
为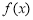 在点
在点 处的导数,
处的导数,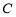 为常数).
为常数).
(1)求函数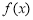 的单调区间
的单调区间
(2)设函数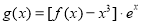 ,若函数
,若函数 在
在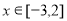 上单调,求实数
上单调,求实数 的取值范围.
的取值范围.
(1)详见解析;(2) c ?11或c ? –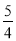
【解析】
试题分析:(1) 将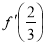 的值代入
的值代入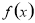 的解析式,列出
的解析式,列出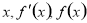 的变化情况表,根据表求出函数
的变化情况表,根据表求出函数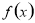 的单调区间.
的单调区间.
(2)求出函数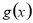 的导数,构造函数
的导数,构造函数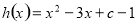 ,分函数递增和递减两类,令
,分函数递增和递减两类,令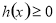 和
和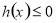 在
在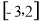 上恒成立,求出C的范围.
上恒成立,求出C的范围.
试题解析:(1)由 ,得
,得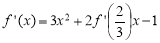 .
.
取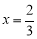 ,得
,得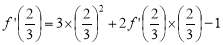 ,
,
解之,得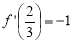 ,
,
因为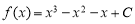 .
.
从而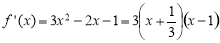 ,列表如下:
,列表如下:
|
|
|
| 1 |
|
| + | 0 | - | 0 | + |
| ↗ | 有极大值 | ↘ | 有极小值 | ↗ |
∴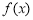 的单调递增区间是
的单调递增区间是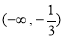 和
和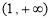 ;
;
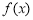 的单调递减区间是
的单调递减区间是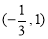 .
.
(3)函数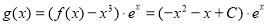 ,
,
有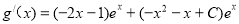 =(–x2– 3 x+C–1)ex,
=(–x2– 3 x+C–1)ex,
当函数在区间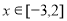 上为单调递增时,等价于h(x)= –x2– 3 x+C–1?0在
上为单调递增时,等价于h(x)= –x2– 3 x+C–1?0在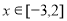 上恒成立, 只要h(2)?0,解得c ?11,
上恒成立, 只要h(2)?0,解得c ?11,
当函数在区间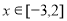 上为单调递减时,等价于h(x)= –x2– 3 x+C–1?0在
上为单调递减时,等价于h(x)= –x2– 3 x+C–1?0在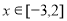 上恒成立, 即
上恒成立, 即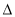 =
=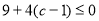 ,解得c ? –
,解得c ? –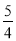 ,
,
所以c的取值范围是c ?11或c ? –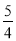 .
.
考点:1.利用导数研究函数的单调性;2.函数恒成立问题.


科目:高中数学 来源:2015届黑龙江省高二下学期期末考试文科数学试卷(解析版) 题型:选择题
以下有关命题的说法错误的是( )
A.命题“若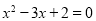 则x=1”的逆否命题为“若
则x=1”的逆否命题为“若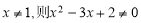 ”
”
B.“ ”是“
”是“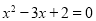 ”的充分不必要条件
”的充分不必要条件
C.若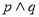 为假命题,则p、q均为假命题
为假命题,则p、q均为假命题
D.对于命题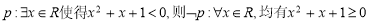
查看答案和解析>>
科目:高中数学 来源:2015届黑龙江省高二下学期期末文科数学试卷(解析版) 题型:选择题
设非零向量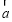 、
、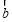 、
、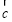 满足|
满足|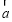 |=|
|=|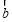 |=|
|=|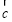 |,
|,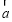 +
+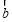 =
=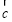 ,则向量
,则向量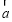 、
、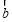 间的夹角为( )
间的夹角为( )
A.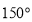 B.
B.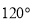 C.
C.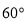 D.
D.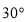
查看答案和解析>>
科目:高中数学 来源:2015届黑龙江大庆铁人中学高二下学期四月月考文科数学试卷(解析版) 题型:解答题
已知曲线C :
: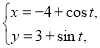 (t为参数), C
(t为参数), C :
: (
(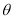 为参数)。
为参数)。
(1)化C ,C
,C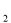 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;
(2)若C 上的点P对应的参数为
上的点P对应的参数为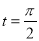 ,Q为C
,Q为C 上的动点,求
上的动点,求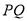 中点
中点 到直线
到直线
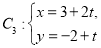 (t为参数)距离的最小值。
(t为参数)距离的最小值。
查看答案和解析>>
科目:高中数学 来源:2015届黑龙江大庆铁人中学高二下学期四月月考文科数学试卷(解析版) 题型:选择题
直线的参数方程为 (t为参数),则直线的倾斜角为( )
(t为参数),则直线的倾斜角为( )
A.40° B.50° C.140° D.130°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com