

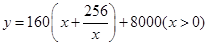 �����Ϊ13120Ԫ����2�����䳤Ϊ15m����Ϊ10.67mʱ����ʹ��������
�����Ϊ13120Ԫ����2�����䳤Ϊ15m����Ϊ10.67mʱ����ʹ��������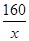 ������
������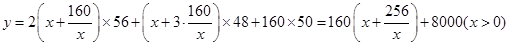 .��
.��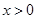 ʱ��
ʱ��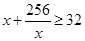 �����ҽ���
�����ҽ���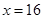 ʱȡ�Ⱥţ���ʱ
ʱȡ�Ⱥţ���ʱ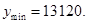 ��2����Ϊ����ij�������15�ף���������12�ף����ԣ�1���еȺŲ�����.��ӵ������Ͽ�����ֵ. ��Ϊ
��2����Ϊ����ij�������15�ף���������12�ף����ԣ�1���еȺŲ�����.��ӵ������Ͽ�����ֵ. ��Ϊ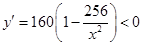 ������
������ ��
��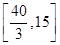 �ϵ����ݼ�����
�ϵ����ݼ�����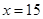 ʱ��y��С����ʱ��=
ʱ��y��С����ʱ��=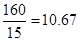 .
.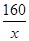 ��
��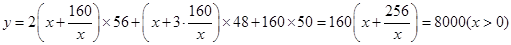 4��
4��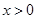 ʱ��
ʱ��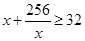 �����ҽ���
�����ҽ���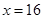 ʱȡ
ʱȡ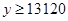
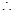 ����ij�Ϊ16mʱ����������Ϊ13120Ԫ 8��
����ij�Ϊ16mʱ����������Ϊ13120Ԫ 8��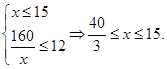 10��
10��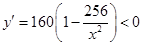 ��
�� ��
��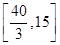 �ϵ����ݼ�����
�ϵ����ݼ�����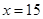 ʱ��y��С����ʱ��=
ʱ��y��С����ʱ��=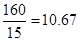 .
.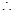 ���䳤Ϊ15m����Ϊ10.67mʱ����ʹ�������� 16��
���䳤Ϊ15m����Ϊ10.67mʱ����ʹ�������� 16��


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ ���ͣ������
 ��
�� ������
������ ��
�� Ϊ��Ȼ�����ĵ�����
Ϊ��Ȼ�����ĵ����� ��
�� ��������
�������� ��ֱ��
��ֱ�� ��ֱ����
��ֱ���� ��ֵ��
��ֵ�� ��
�� �ϵ���Сֵ��
�ϵ���Сֵ�� ��ʹ��
��ʹ�� ��
�� ������
������ �Ͼ�����ͬ�ĵ����ԣ����ܴ��ڣ�˵������
�Ͼ�����ͬ�ĵ����ԣ����ܴ��ڣ�˵������ ���ص㣬��ָ��
���ص㣬��ָ�� ��
�� ������
������ �ϵĵ����ԣ������ܴ��ڣ���˵�����ɣ�
�ϵĵ����ԣ������ܴ��ڣ���˵�����ɣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
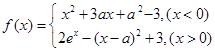 ��
��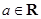 ��
��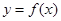 ��
��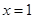 ��ȡ�ü�ֵ����
��ȡ�ü�ֵ����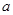 ��ֵ��
��ֵ��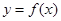 ��ͼ���ϴ����������ԭ��Գƣ���
��ͼ���ϴ����������ԭ��Գƣ���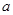 �ķ�Χ��
�ķ�Χ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
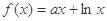 ������a������
������aΪ������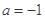 ʱ����
ʱ����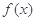 �����ֵ��
�����ֵ��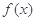 �����䣨0��e���ϵ����ֵΪ
�����䣨0��e���ϵ����ֵΪ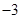 ����a��ֵ��
����a��ֵ��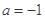 ʱ�����ƶϷ���
ʱ�����ƶϷ���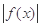 =
=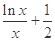 �Ƿ���ʵ���⣮
�Ƿ���ʵ���⣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
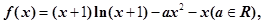
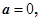 ����
����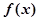 �ļ�ֵ�㼰��Ӧ�ļ�ֵ��
�ļ�ֵ�㼰��Ӧ�ļ�ֵ��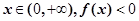 ���������ʵ��
���������ʵ��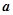 ��ȡֵ��Χ��
��ȡֵ��Χ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
| A��O | B����1 | C���� | D������ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
 (a+b-|a-b|)���������
(a+b-|a-b|)��������� ,��ô
,��ô �����ֵΪ ��
�����ֵΪ ���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com