
分析 (1)化简3an+1+anan+1=3an可得$\frac{1}{{a}_{n+1}}$-$\frac{1}{{a}_{n}}$=$\frac{1}{3}$,从而证明;
(2)由(1)知$\frac{1}{{a}_{n}}$=$\frac{n}{3}$,从而求得bn=anan+1=3($\frac{1}{n}$-$\frac{1}{n+1}$),从而求其前n项和.
解答 解:(1)证明:∵3an+1+anan+1=3an,
∴an+1(3+an)=3an,
又∵a1=3,∴an≠0;
∴$\frac{3}{{a}_{n}}$+1=$\frac{3}{{a}_{n+1}}$,
∴$\frac{1}{{a}_{n+1}}$-$\frac{1}{{a}_{n}}$=$\frac{1}{3}$,
故数列{$\frac{1}{{a}_{n}}$}是以$\frac{1}{3}$为首项,$\frac{1}{3}$为公差的等差数列;
(2)由(1)知$\frac{1}{{a}_{n}}$=$\frac{1}{3}$+(n-1)$\frac{1}{3}$=$\frac{n}{3}$,
故an=$\frac{3}{n}$,
故bn=anan+1=$\frac{3}{n}$•$\frac{3}{n+1}$=3($\frac{1}{n}$-$\frac{1}{n+1}$),
故Sn=3(1-$\frac{1}{2}$)+3($\frac{1}{2}$-$\frac{1}{3}$)+3($\frac{1}{3}$-$\frac{1}{4}$)+…+3($\frac{1}{n}$-$\frac{1}{n+1}$)=$\frac{3n}{n+1}$.
点评 本题考查了数列的构造方法及裂项求和法的应用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
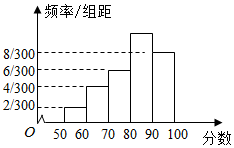 某校为了解一个英语教改实验班的情况,举行了一次测试,将该班30位学生的英语成绩进行统计,得图示频率分布直方图,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].
某校为了解一个英语教改实验班的情况,举行了一次测试,将该班30位学生的英语成绩进行统计,得图示频率分布直方图,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{2\sqrt{14}}{7}$,$\frac{3\sqrt{2}}{2}$] | B. | [$\frac{2\sqrt{14}}{7}$,$\sqrt{2}$) | C. | [$\sqrt{2}$,$\frac{3\sqrt{2}}{2}$] | D. | [$\frac{3\sqrt{2}}{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com