
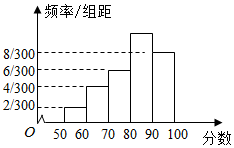
 某校为了解一个英语教改实验班的情况,举行了一次测试,将该班30位学生的英语成绩进行统计,得图示频率分布直方图,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].
某校为了解一个英语教改实验班的情况,举行了一次测试,将该班30位学生的英语成绩进行统计,得图示频率分布直方图,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].分析 (1)英语成绩在[80,90)区间内对应的小矩形最高,由此能求出该班学生英语成绩的众数,由频率分布直方图得该班学生英语成绩的平均数.
(2)成绩低于80分的学生有12人,其中成绩在成绩在[50,60)的学生有2人,成绩为[60,80)的学生有10人,设抽取2人的总绩点分为ξ,则ξ的可能取值为2,3,4,分别求出相应的概率,由此能求出ξ的分布列和Eξ.
解答 解:(1)∵英语成绩在[80,90)区间内对应的小矩形最高,
∴该班学生英语成绩的众数为85.
由频率分布直方图得该班学生英语成绩的平均数为:
$55×\frac{2}{30}+65×\frac{4}{30}+75×\frac{6}{30}+85×\frac{10}{30}+95×\frac{8}{30}$=81.
(2)成绩低于80分的学生有30×($\frac{2}{30}+\frac{4}{30}+\frac{6}{30}$)=12人,
其中成绩在成绩在[50,60)的学生有$30×\frac{2}{30}$=2人,
成绩为[60,80)的学生有$30×(\frac{4}{30}+\frac{6}{30})$=10人,
设抽取2人的总绩点分为ξ,则ξ的可能取值为2,3,4,
P(ξ=2)=$\frac{{C}_{2}^{2}}{{C}_{12}^{2}}$=$\frac{1}{66}$,
P(ξ=3)=$\frac{{C}_{2}^{1}{C}_{10}^{1}}{{C}_{12}^{2}}$=$\frac{20}{66}$,
P(ξ=4)=$\frac{{C}_{10}^{2}}{{C}_{12}^{2}}$=$\frac{45}{66}$,
∴ξ的分布列为:
| ξ | 2 | 3 | 4 |
| P | $\frac{1}{66}$ | $\frac{20}{66}$ | $\frac{45}{66}$ |
点评 本题考查英语成绩的众数及平均数的求法,考查离散型随机变量的分布列、数学期望的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{12}$ | B. | $\frac{7}{12}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2} | B. | {2,4,8} | C. | {1,2,4} | D. | {1,2,4,8} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 24种 | B. | 12种 | C. | 10种 | D. | 9种 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知直线l:x=5,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点F,A是椭圆C上任意一点,|AF|的最小值为$\sqrt{5}$-1,且点A到直线l的距离最小值为5-$\sqrt{5}$.
已知直线l:x=5,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点F,A是椭圆C上任意一点,|AF|的最小值为$\sqrt{5}$-1,且点A到直线l的距离最小值为5-$\sqrt{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com