
 已知直线l:x=5,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点F,A是椭圆C上任意一点,|AF|的最小值为$\sqrt{5}$-1,且点A到直线l的距离最小值为5-$\sqrt{5}$.
已知直线l:x=5,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点F,A是椭圆C上任意一点,|AF|的最小值为$\sqrt{5}$-1,且点A到直线l的距离最小值为5-$\sqrt{5}$.分析 (1)由题意可得5-a=5-$\sqrt{5}$,解得a=$\sqrt{5}$.可得a-c=$\sqrt{5}$-1,即有c=1,由a,b,c的关系,可得b,可得椭圆方程;
(2)将直线y=kx+m代入4x2+5y2=20,运用直线和椭圆相切的条件:判别式为0,求得P的坐标,设M(t,0),又Q(5,5k+m),运用向量的坐标,由以线段PQ为直径的圆经过x轴上的定点,可得$\overrightarrow{MP}$•$\overrightarrow{MQ}$=0,由恒成立思想即可得到定点.
解答 解:(1)由点A到直线l的距离最小值为5-$\sqrt{5}$,
可得5-a=5-$\sqrt{5}$,解得a=$\sqrt{5}$.
又|AF|的最小值为$\sqrt{5}$-1,可得
a-c=$\sqrt{5}$-1,即有c=1,b=$\sqrt{{a}^{2}-{c}^{2}}$=2,
即有椭圆方程为$\frac{{x}^{2}}{5}$+$\frac{{y}^{2}}{4}$=1;
(2)将直线y=kx+m代入4x2+5y2=20,
可得(4+5k2)x2+10kmx+5m2-20=0,
由△=100k2m2-4(4+5k2)(5m2-20)=0,
即m2=4+5k2,
xP=-$\frac{5km}{4+5{k}^{2}}$,yP=kxP+m=$\frac{4}{m}$,即P(-$\frac{5km}{4+5{k}^{2}}$,$\frac{4}{m}$),
设M(t,0),又Q(5,5k+m),$\overrightarrow{MP}$=(-$\frac{5k}{m}$-t,$\frac{4}{m}$),$\overrightarrow{MQ}$=(5-t,5k+m),
即有$\overrightarrow{MP}$•$\overrightarrow{MQ}$=(-$\frac{5k}{m}$-t)(5-t)+$\frac{4}{m}$(5k+m)=t2-5t+4+$\frac{5k}{m}$(t-1),
以线段PQ为直径的圆是否经过x轴上的定点,可得
$\overrightarrow{MP}$•$\overrightarrow{MQ}$=0,即有$\left\{\begin{array}{l}{{t}^{2}-5t+4=0}\\{t-1=0}\end{array}\right.$,解得t=1.
故存在点M(1,0)满足题意.
点评 本题考查椭圆方程的求法,注意最小值的运用,考查定点的求法,注意运用直线和椭圆相切的条件:判别式为0,考查向量垂直的条件:数量积为0,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图几何体中,长方形ACDF所在平面与梯形BCDE所在平面垂直,且BC=2DE,DE∥BC,BD⊥AD,M为AB的中点..
如图几何体中,长方形ACDF所在平面与梯形BCDE所在平面垂直,且BC=2DE,DE∥BC,BD⊥AD,M为AB的中点..查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x<1} | B. | {x|0<x<1} | C. | {x|0<x≤1} | D. | {x|x>1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
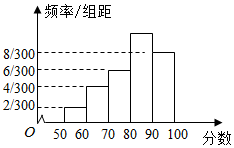 某校为了解一个英语教改实验班的情况,举行了一次测试,将该班30位学生的英语成绩进行统计,得图示频率分布直方图,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].
某校为了解一个英语教改实验班的情况,举行了一次测试,将该班30位学生的英语成绩进行统计,得图示频率分布直方图,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1+$\sqrt{3}$ | C. | $\frac{3}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $12\sqrt{2}$ | B. | $2\sqrt{2}$ | C. | $3\sqrt{2}$ | D. | $4\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com