
| A. | $\frac{5}{12}$ | B. | $\frac{7}{12}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
分析 由直线ax-by=0的倾斜角大于$\frac{π}{4}$,得到a>b.由此能求出直线ax-by=0的倾斜角大于$\frac{π}{4}$的概率.
解答 解:∵直线ax-by=0的倾斜角大于$\frac{π}{4}$,
∴k=$\frac{a}{b}>tan\frac{π}{4}$=1,
∴a>b.
∵投掷一颗骰子两次,将得到的点数依次记为a,b,
∴基本事件总数n=6×6=36,
其中a>b包含的基本事件个数m=${C}_{6}^{2}$=15,
∴直线ax-by=0的倾斜角大于$\frac{π}{4}$的概率为p=$\frac{m}{n}$=$\frac{15}{36}$=$\frac{5}{12}$.
故选:A.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | 关于y轴对称 | B. | 关于x轴对称 | C. | 关于直线y=x对称 | D. | 关于原点对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $0或\frac{3}{2}$ | C. | 2或$-\frac{1}{4}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
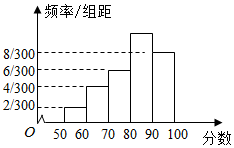 某校为了解一个英语教改实验班的情况,举行了一次测试,将该班30位学生的英语成绩进行统计,得图示频率分布直方图,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].
某校为了解一个英语教改实验班的情况,举行了一次测试,将该班30位学生的英语成绩进行统计,得图示频率分布直方图,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com