
 ,把数列
,把数列 的各项排成如图所示的三角形状,记
的各项排成如图所示的三角形状,记 表示第i行中第j个数,则结论
表示第i行中第j个数,则结论
 ;
; ;
; ;
; .
.

 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源:不详 题型:单选题
 ,cn+1=
,cn+1= ,则( )
,则( )| A.{Sn}为递减数列 |
| B.{Sn}为递增数列 |
| C.{S2n-1}为递增数列,{S2n}为递减数列 |
| D.{S2n-1}为递减数列,{S2n}为递增数列 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 ,[ an]表示an的整数部分,(an)表示an的小数部分,an+1="[" an]+
,[ an]表示an的整数部分,(an)表示an的小数部分,an+1="[" an]+ (
( ),数列{bn}中,b1=1,b2=2,
),数列{bn}中,b1=1,b2=2, (
( ),则a1b1+ a2b2+…+anbn=
),则a1b1+ a2b2+…+anbn= 查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| | 第1列 | 第2列 | 第3列 | 第4列 | 第5列 |
| 第一行 | | 2 | 4 | 6 | 8 |
| 第二行 | 16 | 14 | 12 | 10 | |
| 第三行 | | 18 | 20 | 22 | 24 |
| … | | … | 28 | 26 | |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
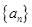 是各项均不为
是各项均不为 的等差数列,公差为
的等差数列,公差为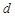 ,
,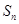 为其前
为其前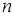 项和,且满足
项和,且满足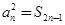 ,
,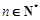 .数列
.数列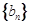 满足
满足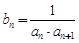 ,
,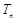 为数列
为数列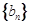 的前
的前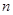 项和.
项和.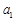 、
、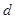 和
和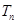 ;
;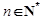 ,不等式
,不等式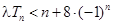 恒成立,求实数
恒成立,求实数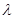 的取值范围;
的取值范围;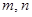
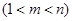 ,使得
,使得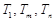 成等比数列?若存在,求出所有
成等比数列?若存在,求出所有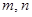 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com