
如图: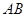 是⊙
是⊙ 的直径,
的直径,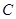 是弧
是弧 的中点,
的中点, ⊥
⊥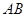 ,垂足为
,垂足为 ,
, 交
交 于点
于点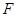 .
.
(1)求证: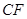 =
=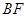 ;
;
(2)若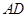 =4,⊙
=4,⊙ 的半径为6,求
的半径为6,求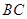 的长.
的长.
(1)证明见解析;(2) .
.
解析试题分析:(1)要证 ,只要证
,只要证 ,一种方法这两个角能否放在一对全等三角形中,为此我们连接
,一种方法这两个角能否放在一对全等三角形中,为此我们连接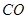 交
交 于
于 ,由圆的性质知
,由圆的性质知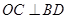 ,这里就有
,这里就有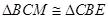 ,要证的角对应相等了,当然也可以证明RtΔCEO≌RtΔBMO,从而
,要证的角对应相等了,当然也可以证明RtΔCEO≌RtΔBMO,从而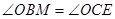 ,也能得到
,也能得到 ,由于在圆中.我们还可以
,由于在圆中.我们还可以 交圆于点
交圆于点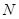 ,可得到到
,可得到到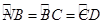 ,那么等弧所对的圆周角相等,结论得证;(2)由(1)可知
,那么等弧所对的圆周角相等,结论得证;(2)由(1)可知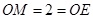 ,下面在
,下面在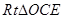 中可求得
中可求得 ,在
,在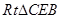 中可求得
中可求得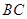 .
.
试题解析:(1)证法一:连接CO交BD于点M,如图1 1分
∵C为弧BD的中点,∴OC⊥BD
又∵OC=OB,∴RtΔCEO≌RtΔBMO 2分
∴∠OCE=∠OBM 3分
又∵OC=OB,∴∠OCB=∠OBC 4分
∴∠FBC=∠FCB,∴CF=BF 5分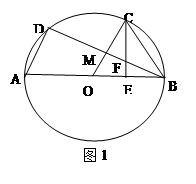
证法二:延长CE交圆O于点N,连接BN,如图2 1分
∵AB是直径且CN⊥AB于点E
∴∠NCB=∠CNB 2分
又∵弧CD=弧BC,∴∠CBD=∠CNB 3分
∴∠NCB=∠CBD
即∠FCB=∠CBF 4分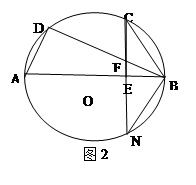
∴CF=BF 5分
(2)∵O,M分别为AB,BD的中点
∴OM=2=OE
∴EB=4 7分
在Rt△COE中, 9分
9分
∴在Rt△CEB中, 10分
10分
考点:(1)证明线段相等;(2)求线段的长.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
如图,在平行四边形ABCD中,E是CD的延长线上一点,BE与AD交于点F,DE=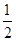 CD.
CD.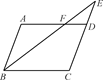
(1)求证:△ABF∽△CEB;
(2)若△DEF的面积为2,求平行四边形ABCD的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于点D.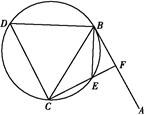
(1)证明:DB=DC;
(2)设圆的半径为1,BC= ,延长CE交AB于点F,求△BCF外接圆的半径.
,延长CE交AB于点F,求△BCF外接圆的半径.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图所示,在直角梯形ABCD中,∠A=∠B=90°,AD∥BC,E为AB上的点,DE平分∠ADC,CE平分∠BCD,以AB为直径的圆与CD有怎样的位置关系?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com