解:(1)∵f(x•y)=f(x)+f(y),
∴f(1)=f(1×1)=f(1)+f(1)=2f(1),
∴f(1)=0.
设x
1,x
2∈(0,+∞)且x
1<x
2,
则

>1,
∴f(

)>0,
∴f(x
1)-f(x
2)=f(x
1)-f(

•x
1)=f(x
1)-f(

)-f(x
1)=-f(

)<0
∴f(x
1)<f(x
2),
∴f(x)在(0,+∞)上是增函数.
(2)令x=

,y=1得,f(

×1)=f(

)+f(1),∴f(1)=0.
令x=3,y=

得,f(1)=f(3×

)=f(3)+f(

),
∵f(

)=-1,∴f(3)=1.
令x=y=3得,f(9)=f(3)+f(3)=2,
∴f(x)-f(
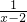
)>f(9),f(x)>f(
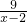
)
∴

,
解得x>1+

.
∴x的取值范围为(1+

,+∞)
分析:(1)由f(x•y)=f(x)+f(y),知f(1)=f(1×1)=f(1)+f(1)=2f(1),由此能求出f(1).设x
1,x
2∈(0,+∞)且x
1<x
2,则

>1,故f(

)>0,由此导出f(x
1)-f(x
2)=f(x
1)-f(

•x
1)=-f(

)<0,从而能够证明f(x)在(0,+∞)上是增函数.
(2)令x=

,y=1,得f(1)=0.令x=3,y=

,得f(3)=1.令x=y=3,得f(9)=2,故f(x)-f(
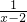
)≥f(9),f(x)≥f(
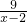
),由此能求出x的范围.
点评:本题考查抽象函数的性质和应用,综合性强,难度大,对数学思维的要求较高,解题时要认真审题,仔细解答,注意合理地进行等价转化.

 )=-1,求满足不等式f(x)-f(
)=-1,求满足不等式f(x)-f(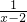 )>2的x的取值范围.
)>2的x的取值范围. >1,
>1, )>0,
)>0, •x1)=f(x1)-f(
•x1)=f(x1)-f( )-f(x1)=-f(
)-f(x1)=-f( )<0
)<0 ,y=1得,f(
,y=1得,f( ×1)=f(
×1)=f( )+f(1),∴f(1)=0.
)+f(1),∴f(1)=0. 得,f(1)=f(3×
得,f(1)=f(3× )=f(3)+f(
)=f(3)+f( ),
), )=-1,∴f(3)=1.
)=-1,∴f(3)=1.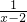 )>f(9),f(x)>f(
)>f(9),f(x)>f(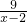 )
) ,
, .
. ,+∞)
,+∞) >1,故f(
>1,故f( )>0,由此导出f(x1)-f(x2)=f(x1)-f(
)>0,由此导出f(x1)-f(x2)=f(x1)-f( •x1)=-f(
•x1)=-f( )<0,从而能够证明f(x)在(0,+∞)上是增函数.
)<0,从而能够证明f(x)在(0,+∞)上是增函数. ,y=1,得f(1)=0.令x=3,y=
,y=1,得f(1)=0.令x=3,y= ,得f(3)=1.令x=y=3,得f(9)=2,故f(x)-f(
,得f(3)=1.令x=y=3,得f(9)=2,故f(x)-f(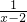 )≥f(9),f(x)≥f(
)≥f(9),f(x)≥f(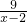 ),由此能求出x的范围.
),由此能求出x的范围.

