
【题目】划船运动员8人,其中3人只会划右舷,2人只会划左舷,3人左右舷都会划,现在要从这8人中选6个人,3个划右舷,3个划左舷,共有多少种选法?
科目:高中数学 来源: 题型:
【题目】如图,三棱锥![]() 中,底面△
中,底面△![]() 是边长为2的正三角形,
是边长为2的正三角形,![]() ,
,![]() 底面
底面![]() ,点
,点![]() 分别为
分别为![]() ,
,![]() 的中点.
的中点.
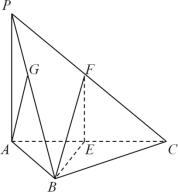
(1)求证:平面![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使得三棱锥
,使得三棱锥![]() 体积为
体积为![]() ?若存在,确定点
?若存在,确定点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图1是某县参加2007年高考的学生身高条形统计图,从左到右的各条形图表示学生人数依次记为A1、A2、…A10(如A2表示身高(单位:cm)在[150,155![]() 内的人数].图2是统计图1中身高在一定范围内学生人数的一个算法流程图.现要统计身高在160~180cm(含160cm,不含180cm)的学生人数,那么在流程图中的判断框内应填写的条件是
内的人数].图2是统计图1中身高在一定范围内学生人数的一个算法流程图.现要统计身高在160~180cm(含160cm,不含180cm)的学生人数,那么在流程图中的判断框内应填写的条件是


A.i<6B.i<7C.i<8D.i<9
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,过点
,过点![]() 且不过点
且不过点![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点,直线
两点,直线![]() 与直线
与直线![]() 交于点
交于点![]() .
.
(Ⅰ)若![]() 垂直于
垂直于![]() 轴,求直线
轴,求直线![]() 的斜率;
的斜率;
(Ⅱ)试判断直线![]() 与直线
与直线![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
,![]() )的周期为
)的周期为![]() ,图像的一个对称中心为
,图像的一个对称中心为![]() ,将函数
,将函数![]() 图像上的所有点的横坐标伸长为原来的2倍(纵坐标不变),在将所得图像向右平移
图像上的所有点的横坐标伸长为原来的2倍(纵坐标不变),在将所得图像向右平移![]() 个单位长度后得到函数
个单位长度后得到函数![]() 的图像.
的图像.
(1)求函数![]() 与
与![]() 的解析式;
的解析式;
(2)是否存在![]() ,使得
,使得![]() ,
,![]() ,
,![]() 按照某种顺序成等差数列?若存在,请确定
按照某种顺序成等差数列?若存在,请确定![]() 的个数;若不存在,说明理由.
的个数;若不存在,说明理由.
(3)求实数a与正整数n,使得![]() 在
在![]() 内恰有2013个零点.
内恰有2013个零点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若有平面![]() 与
与![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,则下列命题中真命题的序号有________.(1)过点
,则下列命题中真命题的序号有________.(1)过点![]() 且垂直于
且垂直于![]() 的直线平行于
的直线平行于![]() ;(2)过点
;(2)过点![]() 且垂直于
且垂直于![]() 的平面垂直于
的平面垂直于![]() ;(3)过点
;(3)过点![]() 且垂直于
且垂直于![]() 的直线在
的直线在![]() 内;(4)过点
内;(4)过点![]() 且垂直于
且垂直于![]() 的直线在
的直线在![]() 内.
内.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对有![]() 个元素的总体
个元素的总体![]() 进行抽样,先将总体分成两个子总体
进行抽样,先将总体分成两个子总体![]() 和
和![]() (m是给定的正整数,且
(m是给定的正整数,且![]() ),再从每个子总体中各随机抽取2个元素组成样本,用
),再从每个子总体中各随机抽取2个元素组成样本,用![]() 表示元素i和j同时出现在样本中的概率,则
表示元素i和j同时出现在样本中的概率,则![]() _________;所有
_________;所有![]() 的和等于________.
的和等于________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市随机选取![]() 位顾客,记录了他们购买甲、乙、丙、丁四种商品的情况,整理成如下统计表,其中“√”表示购买,“×”表示未购买.
位顾客,记录了他们购买甲、乙、丙、丁四种商品的情况,整理成如下统计表,其中“√”表示购买,“×”表示未购买.
| 甲 | 乙 | 丙 | 丁 |
| √ | × | √ | √ |
| × | √ | × | √ |
| √ | √ | √ | × |
| √ | × | √ | × |
85 | √ | × | × | × |
| × | √ | × | × |
(Ⅰ)估计顾客同时购买乙和丙的概率;
(Ⅱ)估计顾客在甲、乙、丙、丁中同时购买![]() 中商品的概率;
中商品的概率;
(Ⅲ)如果顾客购买了甲,则该顾客同时购买乙、丙、丁中那种商品的可能性最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com