
已知函数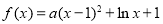 .
.
(1)当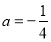 时,求函数
时,求函数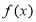 的极值;
的极值;
(2)若函数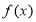 在区间
在区间 上是减函数,求实数
上是减函数,求实数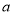 的取值范围;
的取值范围;
(3)当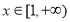 时,函数
时,函数 图像上的点都在
图像上的点都在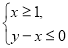 所表示的平面区域内,求实数
所表示的平面区域内,求实数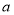 的取值范围.
的取值范围.
(1)当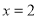 时,函数
时,函数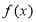 取得极大值
取得极大值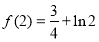 ;(2)
;(2)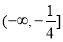 ;(3)
;(3)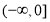 .
.
【解析】
试题分析:(1)将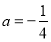 代入函数解析式,直接利用导数求出函数
代入函数解析式,直接利用导数求出函数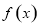 的单调递增区间和递减区间,从而可确定函数
的单调递增区间和递减区间,从而可确定函数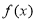 的极值;(2)将条件“
的极值;(2)将条件“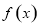 在区间
在区间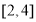 上为减函数”等价转化为“不等式
上为减函数”等价转化为“不等式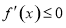 在区间
在区间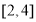 上恒成立”,结合参数分离法进一步转化为
上恒成立”,结合参数分离法进一步转化为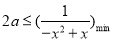 ,从中根据二次函数的图像与性质求出
,从中根据二次函数的图像与性质求出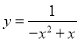 在
在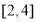 上的最小值即可解决本小问;(3)因函数
上的最小值即可解决本小问;(3)因函数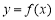 图像上的点都在
图像上的点都在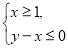 所表示的平面区域内,则当
所表示的平面区域内,则当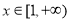 时,不等式
时,不等式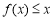 恒成立,即
恒成立,即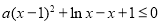 恒成立,设
恒成立,设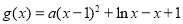 (
(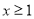 ),只需
),只需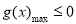 即可,转化思想的运用.
即可,转化思想的运用.
试题解析:(1)当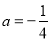 时,
时,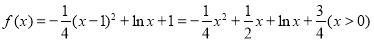
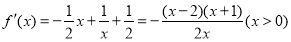
由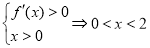 ,由
,由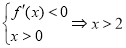
故当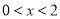 时,
时,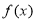 单调递增;当
单调递增;当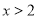 时,
时,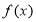 单调递减
单调递减
所以当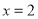 时,函数
时,函数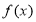 取得极大值
取得极大值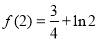 4分
4分
(2)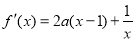 ,∵函数
,∵函数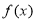 在区间
在区间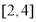 上单调递减
上单调递减
∴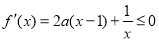 在区间
在区间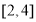 上恒成立,即
上恒成立,即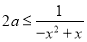 在
在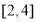 上恒成立,只需
上恒成立,只需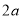 不大于
不大于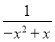 在
在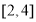 上的最小值即可 6分
上的最小值即可 6分
而
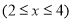 ,则当
,则当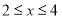 时,
时,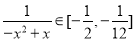
∴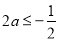 ,即
,即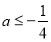 ,故实数
,故实数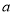 的取值范围是
的取值范围是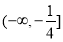 . 8分
. 8分
(3)因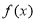 图像上的点在
图像上的点在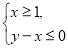 所表示的平面区域内,即当
所表示的平面区域内,即当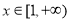 时,不等式
时,不等式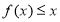 恒成立,即
恒成立,即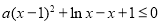 恒成立,设
恒成立,设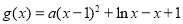 (
(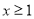 ),只需
),只需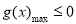 即可.
即可.
由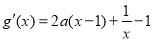
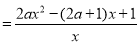 ,
,
(ⅰ)当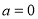 时,
时,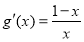 ,当
,当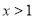 时,
时,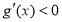 ,函数
,函数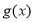 在
在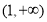 上单调递减,故
上单调递减,故 成立. 9分
成立. 9分
(ⅱ)当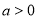 时,由
时,由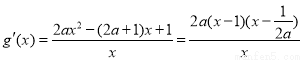 ,令
,令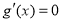 ,得
,得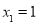 或
或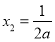 ,
,
①若 ,即
,即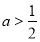 时,在区间
时,在区间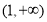 上,
上,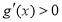 ,函数
,函数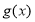 在
在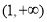 上单调递增,函数
上单调递增,函数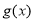 在
在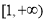 上无最大值,不满足条件;
上无最大值,不满足条件;
②若 ,即
,即 时,函数
时,函数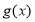 在
在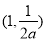 上单调递减,在区间
上单调递减,在区间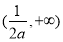 上单调递增,同样
上单调递增,同样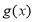 在
在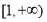 上无最大值,不满足条件. 11分
上无最大值,不满足条件. 11分
(ⅲ)当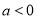 时,由
时,由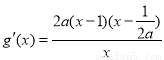 ,因
,因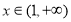 ,故
,故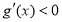 ,则函数
,则函数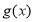 在
在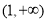 上单调递减,故
上单调递减,故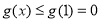 成立.
成立.
综上所述,实数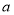 的取值范围是
的取值范围是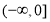 . 12分
. 12分
考点:1.函数的极值与导数;2.函数的单调性与导数;3.函数的最值与导数;4.分离参数法;5.分类讨论的思想.


科目:高中数学 来源:2015届河南省高三上学期第一次月考文科数学试卷(解析版) 题型:选择题
若实数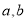 满足
满足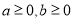 ,且
,且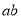 =0,则称a与b互补.记φ(a,b)=
=0,则称a与b互补.记φ(a,b)=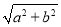 -a-b,那么φ(a,b)=0是a与b互补的( )
-a-b,那么φ(a,b)=0是a与b互补的( )
A.必要而不充分的条件 B.充分而不必要的条件
C.充要条件 D.既不充分也不必要的条件
查看答案和解析>>
科目:高中数学 来源:2015届河北省高二下学期第一次月考理科数学试卷(解析版) 题型:选择题
现安排甲、乙、丙、丁、戊5名同学参加上海世博会志愿者服务活动,每人从事翻译、导游、礼仪、司机四项工作之一,每项工作至少有一人参加.甲、乙、丙不会开车但能从事其他三项工作,丁、戊都能胜四项工作,则不同安排方案的种数是( )
A.240 B.126 C.78 D.72
查看答案和解析>>
科目:高中数学 来源:2015届河北省高二下学期第一次月考文科数学试卷(解析版) 题型:填空题
对于实数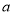 和
和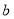 ,定义运算“
,定义运算“ ”:
”: ,设
,设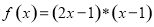 ,且关于
,且关于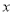 的方程为
的方程为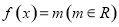 恰有三个互不相等的实数根
恰有三个互不相等的实数根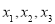 ,则
,则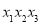 的取值范围是___________.
的取值范围是___________.
查看答案和解析>>
科目:高中数学 来源:2015届河北省高二下学期第一次月考文科数学试卷(解析版) 题型:选择题
已知函数 则
则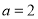 是
是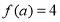 成立的( )
成立的( )
A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2015届河北省唐山市高三年级摸底考试理科数学试卷(解析版) 题型:填空题
在△ABC中,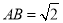 ,点D在边BC上,
,点D在边BC上,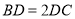 ,
,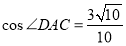 ,
,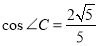 ,则AC+BC=_________________.
,则AC+BC=_________________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com