
【题目】已知函数![]() .
.
(1)判断函数![]() 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(2)若对于任意的![]() 恒成立,求满足条件的实数m的最小值M .
恒成立,求满足条件的实数m的最小值M .
(3)对于(2)中的M,正数a,b满足![]() ,证明:
,证明: ![]() .
.
【答案】(1) 当![]() 时,
时,![]() 为偶函数, 当
为偶函数, 当![]() 时,既不是奇函数也不是偶函数,理由见解析;(2)2;(3) 证明见解析.
时,既不是奇函数也不是偶函数,理由见解析;(2)2;(3) 证明见解析.
【解析】
(1)对![]() 分类讨论,结合奇偶性的定义进行判断可得;
分类讨论,结合奇偶性的定义进行判断可得;
(2)将不等式转化为![]() 对任意的
对任意的![]() 都成立,再构造函数,利用单调性求出最大值即可得到答案;
都成立,再构造函数,利用单调性求出最大值即可得到答案;
(3)由(2)知![]() ,所以
,所以![]() ,再根据
,再根据![]() 变形可证.
变形可证.
(1)(i)当m=1时,![]() ,
,![]() ,
,
因为![]() ,
,
所以![]() 为偶函数;
为偶函数;
(ii)当![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以既不是奇函数也不是偶函数.
(2) 对于任意的![]() ,即
,即![]() 恒成立,
恒成立,
所以![]() 对任意的
对任意的![]() 都成立,
都成立,
设![]() ,
,
则![]() 为
为![]() 上的递减函数,
上的递减函数,
所以![]() 时,
时,![]() 取得最大值1,
取得最大值1,
所以![]() ,即
,即![]() .
.
所以![]() .
.
(3)证明: 由(2)知![]() ,
,
![]() ,所以
,所以![]() ,
,
![]() ,
,
![]() ,当且仅当
,当且仅当![]() 时取等号,①
时取等号,①
又![]()
![]() ,当且仅当
,当且仅当![]() 时取等号,②
时取等号,②
由①②得,![]() ,
,
所以![]() ,
,


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设X~N(μ1,![]() ),Y~N(μ2,
),Y~N(μ2,![]() ),这两个正态分布密度曲线如图所示,下列结论中正确的是 ( )
),这两个正态分布密度曲线如图所示,下列结论中正确的是 ( )

A. P(Y≥μ2)≥P(Y≥μ1)
B. P(X≤σ2)≤P(X≤σ1)
C. 对任意正数t,P(X≥t)≥P(Y≥t)
D. 对任意正数t,P(X≤t)≥P(Y≤t)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合A,B是R中两个子集,对于![]() ,定义:
,定义: 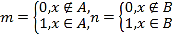 .①若
.①若![]() ;则对任意
;则对任意![]() ;②若对任意
;②若对任意![]() ,则
,则![]() ;③若对任意
;③若对任意![]() ,则A,B的关系为
,则A,B的关系为![]() .上述命题正确的序号是______. (请填写所有正确命题的序号)
.上述命题正确的序号是______. (请填写所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在独立性检验中,统计量![]() 有三个临界值:2.706,3.841和6.635.当
有三个临界值:2.706,3.841和6.635.当![]() 时,有90%的把握说明两个事件有关;当
时,有90%的把握说明两个事件有关;当![]() 时,有95%的把握说明两个事件有关,当
时,有95%的把握说明两个事件有关,当![]() 时,有99%的把握说明两个事件有关,当
时,有99%的把握说明两个事件有关,当![]() 时,认为两个事件无关.在一项打鼾与心脏病的调查中,共调查了2000人,经计算
时,认为两个事件无关.在一项打鼾与心脏病的调查中,共调查了2000人,经计算![]() .根据这一数据分析,认为打鼾与患心脏病之间( )
.根据这一数据分析,认为打鼾与患心脏病之间( )
A. 有95%的把握认为两者有关 B. 约95%的打鼾者患心脏病
C. 有99%的把握认为两者有关 D. 约99%的打鼾者患心脏病
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】交强险是车主必须为机动车购买的险种,若普通![]() 座以下私家车投保交强险的基准保费为
座以下私家车投保交强险的基准保费为![]() 元,在下一年续保时,实行费率浮动机制,保费与车辆发生道路交通事故出险的情况想联系,最终保费
元,在下一年续保时,实行费率浮动机制,保费与车辆发生道路交通事故出险的情况想联系,最终保费![]() 基准保费
基准保费![]() (
(![]() 与道路交通事故相联系的浮动比率),具体情况如下表:
与道路交通事故相联系的浮动比率),具体情况如下表:

为了解某一品牌普通![]() 座以下私家车的投保情况,随机抽取了
座以下私家车的投保情况,随机抽取了![]() 辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况,统计如下表:
辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况,统计如下表:
类型 |
|
|
|
|
|
|
数量 |
|
|
|
|
|
|
若以这![]() 辆该品牌的投保类型的频率代替一辆车投保类型的概率,则随机抽取一辆该品牌车在第四年续保时的费用的期望为( )
辆该品牌的投保类型的频率代替一辆车投保类型的概率,则随机抽取一辆该品牌车在第四年续保时的费用的期望为( )
A. ![]() 元 B.
元 B. ![]() 元 C.
元 C. ![]() 元 D.
元 D. ![]() 元
元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)某食品的保鲜时间y(单位:小时)与储藏温度x(单位:℃)满足函数关系![]() 自然对数的底数,k,b为常数),若该食品在0℃的保鲜时间是192小时,在22℃的保鲜时间是48小时,求该食品在33℃的保鲜时间.
自然对数的底数,k,b为常数),若该食品在0℃的保鲜时间是192小时,在22℃的保鲜时间是48小时,求该食品在33℃的保鲜时间.
(2)某药厂生产一种口服液,按药品标准要求其杂质含量不能超过0.01%,若初始时含杂质0.2%,每次过滤可使杂质含量减少三分之一,问至少应过滤几次才能使得这种液体达到要求?(已知![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com