解:(1)由已知得
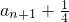
=
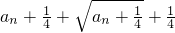
,
∴

,
∵
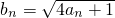
所以b
n+12=b
n2+2b
n+1
∴b
n+1=b
n+1,
所以数列{b
n}为等差数列;
(2)由(1)得:b
n+1=b
n+1且b
1=1,∴b
n=n,
即

,∴
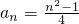
,
∴
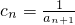
=

,
则


=

;
(3)设存在m,n满足条件,则有1•a
n=a
m2∴

,
即4(n
2-1)=(m
2-1)
2,
所以m
2-1必为偶数,设为2t,
则n
2-1=t
2,∴n
2-t
2=1
∴(n-t)(n+t)=1,
∴有

或

,即n=1,t=0,
∴m
2-1=2t=0,∴m=1与已知矛盾.
∴不存在m,n(m,n∈N
*,m≠n)使得1,a
m,a
n三个数依次成等比数列.
分析:(1)将条件化为

,根据
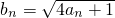
,可得b
n+12=b
n2+2b
n+1,即b
n+1=b
n+1,从而数列{b
n}为等差数列;
(2)由(1)可求数列{b
n}的通项,从而可得

,由此可求数列{a
n}的通项,由于
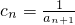
,利用裂项法可求{c
n}前n项的和S
n;
(3)设存在m,n满足条件,则有1•a
n=a
m2,从而可化简为4(n
2-1)=(m
2-1)
2,所以m
2-1必为偶数,设为2t,从而可有n-t)(n+t)=1,所以有

或

,即n=1,t=0,进而引出矛盾,问题得解.
点评:本题以数列的递推式为载体,考查等差数列的定义,考查裂项法求数列的和,同时考查了存在性问题,解题的关键是构造新数列,利用假设存在,转化为封闭型问题.

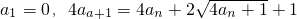 ,令
,令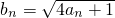 .
.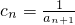 ,求{cn}前n项的和Sn;
,求{cn}前n项的和Sn;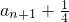 =
=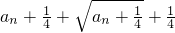 ,
, ,
,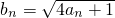
 ,∴
,∴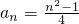 ,
,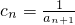 =
= ,
,
 =
= ;
; ,
, 或
或 ,即n=1,t=0,
,即n=1,t=0, ,根据
,根据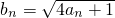 ,可得bn+12=bn2+2bn+1,即bn+1=bn+1,从而数列{bn}为等差数列;
,可得bn+12=bn2+2bn+1,即bn+1=bn+1,从而数列{bn}为等差数列; ,由此可求数列{an}的通项,由于
,由此可求数列{an}的通项,由于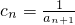 ,利用裂项法可求{cn}前n项的和Sn;
,利用裂项法可求{cn}前n项的和Sn; 或
或 ,即n=1,t=0,进而引出矛盾,问题得解.
,即n=1,t=0,进而引出矛盾,问题得解.

 阅读快车系列答案
阅读快车系列答案