练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知定义在R上的可导函数f（x）的导函数为f′（x），满足f′（x）＜f（x），且f（﹣x）=f（2+x），f（2）=1，则不等式f（x）＜ex的解集为（ ）
    A.（﹣2，+∞）
    B.（0，+∞）
    C.（1，+∞）
    D.（2，+∞）

    【答案】B
    【解析】解：∵f′（x）＜f（x）， ∴f′（x）﹣f（x）＜0，
    令g（x）= ，则g′（x）= ＜0，
    故g（x）在R递减，
    而f（﹣x）=f（2+x），
    则f（1﹣x）=f（1+x），f（x）关于x=1对称，
    则f（2）=f（0）=1，
    由f（x）＜ex ， 得：g（x）= ＜1=g（0），
    解得：x＞0，
    故选：B．
    令g（x）= ，求出函数的导数，求出g（0）=1，从而求出不等式的解集即可．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】将函数 的图象上每点的横坐标缩短到原来的 倍（纵坐标不变），得到函数y=f（x）的图象．
    （1）求函数f（x）的解析式及其图象的对称轴方程；
    （2）在△ABC中，内角A，B，C的对边分别为a，b，c．若 ，求sinB的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知向量 =（2 cosx，cosx）， =（sinx，2cosx）（x∈R），设函数f（x）= ﹣1． （Ⅰ）求函数f（x）的单调减区间；
    （Ⅱ）已知锐角△ABC的三个内角分别为A，B，C，若f（A）=2，B= ，边AB=3，求边BC．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】程序框图如图所示，则该程序运行后输出n的值是（ ）
    A.4
    B.2
    C.1
    D.2017

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在某校组织的“共筑中国梦”竞赛活动中，甲、乙两班各有6名选手参赛，在第一轮笔试环节中，评委将他们的笔试成绩作为样本数据，绘制成如图所示的茎叶图，为了增加结果的神秘感，主持人故意没有给出甲、乙两班最后一位选手的成绩，只是告诉大家，如果某位选手的成绩高于90分（不含90分），则直接“晋级” （Ⅰ）求乙班总分超过甲班的概率
    （Ⅱ）主持人最后宣布：甲班第六位选手的得分是90分，乙班第六位选手的得分是97分
    ①请你从平均分光和方差的角度来分析两个班的选手的情况；
    ②主持人从甲乙两班所有选手成绩中分别随机抽取2个，记抽取到“晋级”选手的总人数为ξ，求ξ的分布列及数学期望．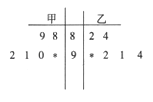

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥S﹣ABCD中，底面ABCD是边长为4的菱形，∠ABC=60°，SA⊥平面ABCD，且SA=4，M在棱SA上，且AM=1，N在棱SD上且SN=2ND． （Ⅰ）求证：CN∥面BDM；
    （Ⅱ）求直线SD与平面BDM所成的角的正弦值．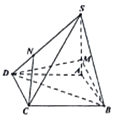

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图1，等腰梯形BCDP中，BC∥PD，BA⊥PD于点A，PD=3BC，且AB=BC=1．沿AB把△PAB折起到△P'AB的位置（如图2），使∠P'AD=90°． （Ⅰ）求证：CD⊥平面P'AC；
    （Ⅱ）求二面角A﹣P'D﹣C的余弦值；
    （Ⅲ）线段P'A上是否存在点M，使得BM∥平面P'CD．若存在，指出点M的位置并证明；若不存在，请说明理由．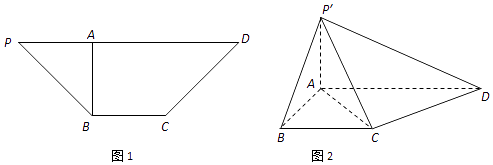

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设D是函数y=f（x）定义域内的一个区间，若存在x0∈D，使f（x0）=﹣x0 ， 则称x0是f（x）的一个“次不动点”，也称f（x）在区间D上存在次不动点．若函数f（x）=ax2﹣3x﹣a+ 在区间[1，4]上存在次不动点，则实数a的取值范围是（ ）
    A.（﹣∞，0）
    B.（0， ）
    C.[ ，+∞）
    D.（﹣∞， ]

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数y=f（x），若在定义域内存在x0 ， 使得f（﹣x0）=﹣f（x0）成立，则称x0为函数f（x）的局部对称点．
    （I）若a∈R且a≠0，求函数f（x）=ax2+x﹣a的“局部对称点”；
    （II）若函数f（x）=4x﹣m2x+1+m2﹣3在R上有局部对称点，求实数m的取值范围．

    查看答案和解析>>

    同步练习册答案