Question

【题目】如图1，等腰梯形BCDP中，BC∥PD，BA⊥PD于点A，PD=3BC，且AB=BC=1．沿AB把△PAB折起到△P'AB的位置（如图2），使∠P'AD=90°． （Ⅰ）求证：CD⊥平面P'AC；
（Ⅱ）求二面角A﹣P'D﹣C的余弦值；
（Ⅲ）线段P'A上是否存在点M，使得BM∥平面P'CD．若存在，指出点M的位置并证明；若不存在，请说明理由．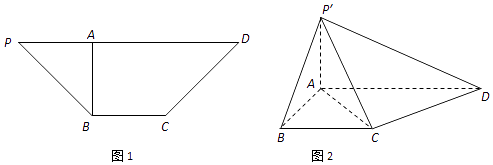

Answer 1

【答案】证明：（Ⅰ）因为∠P'AD=90°，所以P'A⊥AD． 因为在等腰梯形中，AB⊥AP，所以在四棱锥中，AB⊥AP'．
又AD∩AB=A，所以P'A⊥面ABCD．
因为CD面ABCD，所以P'A⊥CD．
因为等腰梯形BCDE中，AB⊥BC，PD=3BC，
且AB=BC=1．
所以 ， ，AD=2．所以AC2+CD2=AD2 ．
所以AC⊥CD．
因为P'A∩AC=A，所以CD⊥平面P'AC．
解：（Ⅱ）由（Ⅰ）知，P'A⊥面ABCD，AB⊥AD，
如图，建立空间直角坐标系，A（0，0，0），B（1，0，0），
C（1，1，0），D（0，2，0），P'（0，0，1）．
所以 ， ．
由（Ⅰ）知，平面P'AD的法向量为 ，
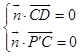设 为平面P'CD的一个法向量，则 ，即 ，
再令y=1，得 ． = = ．
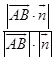所以二面角A﹣P'D﹣C的余弦值为 ．
（Ⅲ）线段P'A上存在点M，使得BM∥平面P'CD．
依题意可设 ，其中0≤λ≤1．所以M（0，0，λ）， ．
由（Ⅱ）知，平面P'CD的一个法向量 ．
因为BM∥平面P'CD，所以 ，
所以 ，解得 ．
所以，线段P'A上存在点M，使得BM∥平面P'CD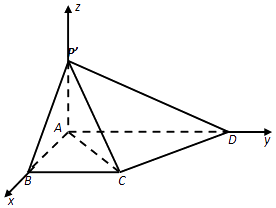

【解析】（Ⅰ）推导出P'A⊥AD，AB⊥AP'，从而P'A⊥面ABCD，进而P'A⊥CD，再推导出AC⊥CD，由此能求出CD⊥平面P'AC．（Ⅱ）推导出P'A⊥面ABCD，AB⊥AD，从而建立空间直角坐标系，求出平面P'AD的法向量和平面P'CD的一个法向量，利用向量法能求出二面角A﹣P'D﹣C的余弦值．（Ⅲ）设 ，利用向量法能求出线段P'A上存在点M，使得BM∥平面P'CD．
【考点精析】认真审题，首先需要了解直线与平面垂直的判定(一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直；注意点：a)定理中的“两条相交直线”这一条件不可忽视；b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想)．