
【题目】已知函数![]() ,无穷数列
,无穷数列![]() 的首项
的首项![]() .
.
(1)如果![]() ,写出数列
,写出数列![]() 的通项公式;
的通项公式;
(2)如果![]() (
(![]() 且
且![]() ),要使得数列
),要使得数列![]() 是等差数列,求首项
是等差数列,求首项![]() 的取值范围;
的取值范围;
(3)如果![]() (
(![]() 且
且![]() ),求出数列
),求出数列![]() 的前
的前![]() 项和
项和![]() .
.
科目:高中数学 来源: 题型:
【题目】一种掷硬币走跳棋的游戏:在棋盘上标有第1站、第2站、第3站、…、第100站,共100站,设棋子跳到第![]() 站的概率为
站的概率为![]() ,一枚棋子开始在第1站,棋手每掷一次硬币,棋子向前跳动一次.若硬币的正面向上,棋子向前跳一站;若硬币的反面向上,棋子向前跳两站,直到棋子跳到第99站(失败)或者第100站(获胜)时,游戏结束.
,一枚棋子开始在第1站,棋手每掷一次硬币,棋子向前跳动一次.若硬币的正面向上,棋子向前跳一站;若硬币的反面向上,棋子向前跳两站,直到棋子跳到第99站(失败)或者第100站(获胜)时,游戏结束.
(1)求![]()
![]()
![]() ;
;
(2)求证:数列![]()
![]() 为等比数列;
为等比数列;
(3)求玩该游戏获胜的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() (
(![]() 、
、![]() 为实常数).
为实常数).
(1)当![]() 时,证明:
时,证明:![]() 不是奇函数;
不是奇函数;
(2)设![]() 是奇函数,求
是奇函数,求![]() 与
与![]() 的值;
的值;
(3)当![]() 是奇函数时,研究是否存在这样的实数集的子集
是奇函数时,研究是否存在这样的实数集的子集![]() ,对任何属于
,对任何属于![]() 的
的![]() 、
、![]() ,都有
,都有![]() 成立?若存在试找出所有这样的
成立?若存在试找出所有这样的![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以O为极点,x轴非负半轴为极轴建立极坐标系圆C的极坐标方程为
中,以O为极点,x轴非负半轴为极轴建立极坐标系圆C的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为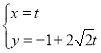 (t为参数),直线
(t为参数),直线![]() 和圆C交于A,B两点,P是圆C上不同于A,B的任意一点.
和圆C交于A,B两点,P是圆C上不同于A,B的任意一点.
(1)求圆C及直线![]() 的直角坐标方程;
的直角坐标方程;
(2)求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() ,且
,且![]() 在
在![]() 上存在零点,求实数
上存在零点,求实数![]() 的取值范围;
的取值范围;
(2)若对任意![]() ,存在
,存在![]() 使
使![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)若存在实数![]() ,使得当
,使得当![]() 时,
时,![]() 恒成立,求实数
恒成立,求实数![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
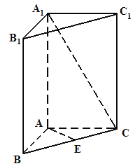
【题目】如图,直三棱柱![]() 的底面
的底面![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,侧棱
,侧棱![]() 底面
底面![]() ,且
,且![]() ,
,![]() 是
是![]() 的中点.
的中点.
(1)求直三棱柱![]() 的全面积;
的全面积;
(2)求异面直线![]() 与
与![]() 所成角
所成角![]() 的大小(结果用反三角函数表示);
的大小(结果用反三角函数表示);
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com