
【题目】已知函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)若![]() 存在两个极值点
存在两个极值点![]() ,证明:
,证明:![]() .
.
【答案】(1)当![]() 时,
时,![]() 在
在![]() 单调递减.,
单调递减.,
当![]() 时,
时, ![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增.
单调递增.
(2)证明见解析.
【解析】分析:(1)首先确定函数的定义域,之后对函数求导,之后对![]() 进行分类讨论,从而确定出导数在相应区间上的符号,从而求得函数对应的单调区间;
进行分类讨论,从而确定出导数在相应区间上的符号,从而求得函数对应的单调区间;
(2)根据![]() 存在两个极值点,结合第一问的结论,可以确定
存在两个极值点,结合第一问的结论,可以确定![]() ,令
,令![]() ,得到两个极值点
,得到两个极值点![]() 是方程
是方程![]() 的两个不等的正实根,利用韦达定理将其转换,构造新函数证得结果.
的两个不等的正实根,利用韦达定理将其转换,构造新函数证得结果.
详解:(1)![]() 的定义域为
的定义域为![]() ,
,![]() .
.
(i)若![]() ,则
,则![]() ,当且仅当
,当且仅当![]() ,
,![]() 时
时![]() ,所以
,所以![]() 在
在![]() 单调递减.
单调递减.
(ii)若![]() ,令
,令![]() 得,
得,![]() 或
或![]() .
.
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .所以
.所以![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增.
单调递增.
(2)由(1)知,![]() 存在两个极值点当且仅当
存在两个极值点当且仅当![]() .
.
由于![]() 的两个极值点
的两个极值点![]() 满足
满足![]() ,所以
,所以![]() ,不妨设
,不妨设![]() ,则
,则![]() .由于
.由于
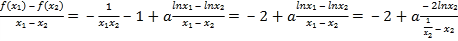 ,
,
所以![]() 等价于
等价于![]() .
.
设函数![]() ,由(1)知,
,由(1)知,![]() 在
在![]() 单调递减,又
单调递减,又![]() ,从而当
,从而当![]() 时,
时,![]() .
.
所以![]() ,即
,即![]() .
.


 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代的数学名著,书中把三角形的田称为“圭田”,把直角梯形的田称为“邪田”,称底是“广”,称高是“正从”,“步”是丈量土地的单位.现有一邪田,广分别为十步和二十步,正从为十步,其内有一块广为八步,正从为五步的圭田.若在邪田内随机种植一株茶树,求该株茶树恰好种在圭田内的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区2008年至2016年粮食产量的部分数据如下表:

(1)求该地区2008年至2016年的粮食年产量![]() 与年份
与年份![]() 之间的线性回归方程;
之间的线性回归方程;
(2)利用(1)中的回归方程,分析2008年至2016年该地区粮食产量的变化情况,并预测该地区 2018年的粮食产量.
附:回归直线的斜率和截距的最小二乘估计公式分别为 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有![]() 个小球,甲、乙两位同学轮流且不放回抓球,每次最少抓1个球,最多抓3个球,规定谁抓到最后一个球赢.如果甲先抓,那么下列推断正确的是_____________.(填写序号)
个小球,甲、乙两位同学轮流且不放回抓球,每次最少抓1个球,最多抓3个球,规定谁抓到最后一个球赢.如果甲先抓,那么下列推断正确的是_____________.(填写序号)
①若![]() ,则甲有必赢的策略; ②若
,则甲有必赢的策略; ②若![]() ,则乙有必赢的策略;
,则乙有必赢的策略;
③若![]() ,则甲有必赢的策略; ④若
,则甲有必赢的策略; ④若![]() ,则乙有必赢的策略.
,则乙有必赢的策略.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com