
 |
| 1≤i<j≤n |
| 2 |
| 3 |
 |
| 1≤i<j≤n |
| 2 |
| 3 |
 |
| 1≤i<j≤3 |
 |
| 1≤i<j≤n |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
 |
| 1≤i<j≤3 |
| 1 |
| 2 |
| x | 2 1 |
| x | 2 2 |
| x | 2 3 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
 |
| 1≤i<j≤n |
| 1 |
| 2 |
| x | 2 1 |
| x | 2 2 |
| x | 2 n |
| 1 |
| 2 |
| n |
| 2 |
| 1 |
| 2 |
| n-1 |
| 2 |
| n-1 |
| 2 |
| n-1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


科目:高中数学 来源: 题型:
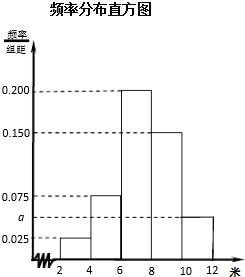 (2013•朝阳区二模)为了解某市今年初二年级男生的身体素质状况,从该市初二年级男生中抽取了一部分学生进行“掷实心球”的项目测试.成绩低于6米为不合格,成绩在6至8米(含6米不含8米)的为及格,成绩在8米至12米(含8米和12米,假定该市初二学生掷实心球均不超过12米)为优秀.把获得的所有数据,分成[2,4),[4,6),[6,8),[8,10),[10,12]五组,画出的频率分布直方图如图所示.已知有4名学生的成绩在10米到12米之间.
(2013•朝阳区二模)为了解某市今年初二年级男生的身体素质状况,从该市初二年级男生中抽取了一部分学生进行“掷实心球”的项目测试.成绩低于6米为不合格,成绩在6至8米(含6米不含8米)的为及格,成绩在8米至12米(含8米和12米,假定该市初二学生掷实心球均不超过12米)为优秀.把获得的所有数据,分成[2,4),[4,6),[6,8),[8,10),[10,12]五组,画出的频率分布直方图如图所示.已知有4名学生的成绩在10米到12米之间.查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| A |
| 2 |
| A |
| 2 |
| A |
| 2 |
| A |
| 2 |
| 5π |
| 12 |
| 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com