
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() ,
,![]() 的极坐标方程分别为
的极坐标方程分别为![]() ,
,![]() .
.
(1)将直线![]() 的参数方程化为极坐标方程,将
的参数方程化为极坐标方程,将![]() 的极坐标方程化为参数方程;
的极坐标方程化为参数方程;
(2)当![]() 时,直线
时,直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,与
两点,与![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() .
.
科目:高中数学 来源: 题型:
【题目】为了进一步提升基层党员自身理论素养,市委组织部举办了党建主题知识竞赛(满分120分),从参加竞赛的党员中采用分层抽样的方法抽取若干名党员,统计他们的竞赛成绩得到下面频率分布表:
成绩/分 |
|
|
|
|
|
频率 | 0.1 | 0.3 | 0.3 | 0.2 | 0.1 |
已知成绩在区间![]() 内的有
内的有![]() 人.
人.
(1)将成绩在![]() 内的定义为“优秀”,在
内的定义为“优秀”,在![]() 内的定义为“良好”,请将
内的定义为“良好”,请将![]() 列联表补充完整.
列联表补充完整.
男党员 | 女党员 | 合计 | |
优秀 | |||
良好 | 15 | ||
合计 | 25 |
(2)判断是否有![]() 的把握认为竞赛成绩是否优秀与性别有关?
的把握认为竞赛成绩是否优秀与性别有关?
(3)若在抽取的竞赛成绩为优秀的党员中任意抽取2人进行党建知识宣讲,求被抽取的这两人成绩都在![]() 内的概率.
内的概率.
附: ![]()
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆形纸片的圆心为O,半径为6cm,该纸片上的正方形ABCD的中心为O.E,F,G,H为圆O上的点,△ABE,△BCF,△CDG,△ADH分别是以AB,BC,CD,DA为底边的等腰三角形.沿虚线剪开后,分别以AB,BC,CD,DA为折痕折起△ABE,△BCF,△CDG,△ADH,使得E,F,G,H重合得到一个四棱锥.当该四棱锥的侧面积是底面积的2倍时,该四棱锥的外接球的表面积为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)已知函数f(x)![]() (2x
(2x![]() ),若f(
),若f(![]() )
)![]() ,θ∈(0,
,θ∈(0,![]() ),求tanθ.
),求tanθ.
(2)若函数g(x)=﹣(![]() sin
sin![]() cos
cos![]() )cos
)cos![]() ,讨论函数g(x)在区间[
,讨论函数g(x)在区间[![]() ,
,![]() 上的单调性.
上的单调性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,![]() φ<0)的图象与y轴的交点为(0,1),它的一个最高点和一个最低点的坐标分别为(x0,2),(x0
φ<0)的图象与y轴的交点为(0,1),它的一个最高点和一个最低点的坐标分别为(x0,2),(x0![]() ,﹣2),
,﹣2),
(1)若函数f(x)的最小正周期为π,求函数f(x)的解析式;
(2)当x∈(x0,x0![]() )时,f(x)图象上有且仅有一个最高点和一个最低点,且关于x的方程f(x)﹣a=0在区间[
)时,f(x)图象上有且仅有一个最高点和一个最低点,且关于x的方程f(x)﹣a=0在区间[![]() ,
,![]() ]上有且仅有一解,求实数a的取值范围.
]上有且仅有一解,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E、F分别为AB、BC的中点,现在沿DE、DF及EF把△ADE、△CDF和△BEF折起,使A、B、C三点重合,重合后的点记为P.

问:(1)这个几何体是什么?
(2)这个几何体由几个面构成?每个面的三角形是什么三角形?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列所给4个图象中,与所给3件事吻合最好的顺序为 ( )
(1)我离开家不久,发现自己把作业本忘在家里了,于是立刻返回家里取了作业本再上学;
(2)我出发后,心情轻松,缓缓行进,后来为了赶时间开始加速;
(3)我骑着车一路以常速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间.
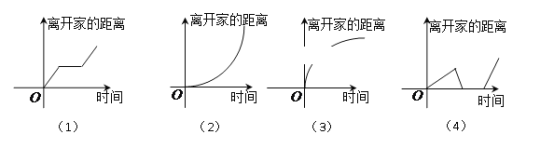
A. (1)(2)(4) B. (4)(2)(1) C. (4)(3)(1) D. (4)(1)(2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示为一正方体的平面展开图,在这个正方体中,有下列四个命题:
①AF⊥GC;
②BD与GC成异面直线且夹角为60;
③BD∥MN;
④BG与平面ABCD所成的角为45.
其中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com