【题目】已知
是双曲线
的右焦点，
是
左支上一点，
），当
周长最小时，则点的纵坐标为（ ）
A. 
B. 
C. 
D. 
【答案】B
【解析】
左焦点E（-3，0）,△APF周长最小|PA|+|PF|最小|PA|+|PE|+2最小P在线段AE上．
如图：
由双曲线C的方程可知：a2=1，b2=8，∴c2=a2+b2=1+8=9，∴c=3，∴左焦点E（-3，0），右焦点F（3，0），
∵|AF|=
，所以当三角形APF的周长最小时，|PA|+|PF|最小．
由双曲线的性质得|PF|-|PE|=2a=2，∴|PF|=|PE|+2，
又|PE|+|PA|≥|AE|=|AF|=15，当且仅当A，P，E三点共线时，等号成立．
∴三角形APF的周长：|AF|+|AP|+|PF|=15+|PE|+|AP|+2≥15+15+2=32．
此时，直线AE的方程为y=
，将其代入到双曲线方程得：x2+9x+14=0，
解得x=-7（舍）或x=-2，
由x=-2得y=2
（负值已舍）
故选：B．
科目：高中数学 来源： 题型：
【题目】[选修4-4：坐标系与参数方程]
在极坐标系中，曲线
的极坐标方程是
，以极点为原点
，极轴为
轴正半轴（两坐标系取相同的单位长度）的直角坐标系
中，曲线
的参数方程为： 
（
为参数）.
（1）求曲线
的直角坐标方程与曲线
的普通方程；
（2）将曲线
经过伸缩变换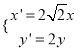
后得到曲线
，若
， 
分别是曲线
和曲线
上的动点，求
的最小值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
，其中常数
．
（1）当
时，求函数
的单调递增区间；
（2）设定义在
上的函数
在点
处的切线方程为
，若
在
内恒成立，则称
为函数
的“类对称点”，当
时，试问
是否存在“类对称点”，若存在，请至少求出一个“类对称点”的横坐标；若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知某地区中小学生人数和近视情况如图1和图2所示.为了解该地区中小学生的近视形成原因，用分层抽样的方法抽取2%的学生作为样本进行调查.
（1）求样本容量和抽取的高中生近视人数分别是多少？
（2）在抽取的
名高中生中，平均每天学习时间超过9小时的人数为
，其中有12名学生近视，请完成高中生平均每天学习时间与近视的列联表：
平均学习时间不超过9小时 | 平均学习时间超过9小时 | 总计 | |
不近视 | |||
近视 | |||
总计 |
（3）根据（2）中的列联表，判断是否有
的把握认为高中生平均每天学习时间与近视有关？
附：
，其中
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】选修4-4：坐标系与参数方程
在平面直角坐标系
中，直线
的参数方程为
（
为参数），以原点
为极点，
轴的正半轴为极轴建立极坐标系，曲线
，
的极坐标方程分别为
，
.
（1）将直线的参数方程化为极坐标方程，将的极坐标方程化为参数方程；
（2）当
时，直线与交于，
两点，与交于，
两点，求
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”（如下图），四个全等的直角三角形（朱实），可以围成一个大的正方形，中空部分为一个小正方形（黄实）．若直角三角形中一条较长的直角边为8，直角三角形的面积为24，若在上面扔一颗玻璃小球，则小球落在“黄实”区域的概率为（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
