
【题目】汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”(如下图),四个全等的直角三角形(朱实),可以围成一个大的正方形,中空部分为一个小正方形(黄实).若直角三角形中一条较长的直角边为8,直角三角形的面积为24,若在上面扔一颗玻璃小球,则小球落在“黄实”区域的概率为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:高中数学 来源: 题型:
【题目】中国有个名句“运筹帷幄之中,决胜千里之外.”其中的“筹”原意是指《孙子算经》中记载的算筹,古代是用算筹来进行计算,算筹是将几寸长的小竹棍摆在平面上进行运算,算筹的摆放形式有纵横两种形式,如下表
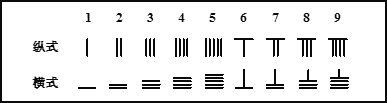
表示一个多位数时,像阿拉伯计数一样,把各个数位的数码从左到右排列,但各位数码的筹式需要纵横相间,个位,百位,万位数用纵式表示,十位,千位,十万位用横式表示,以此类推, 例如6613用算筹表示就是:![]() ,则26337用算筹可表示为( )
,则26337用算筹可表示为( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,![]() φ<0)的图象与y轴的交点为(0,1),它的一个最高点和一个最低点的坐标分别为(x0,2),(x0
φ<0)的图象与y轴的交点为(0,1),它的一个最高点和一个最低点的坐标分别为(x0,2),(x0![]() ,﹣2),
,﹣2),
(1)若函数f(x)的最小正周期为π,求函数f(x)的解析式;
(2)当x∈(x0,x0![]() )时,f(x)图象上有且仅有一个最高点和一个最低点,且关于x的方程f(x)﹣a=0在区间[
)时,f(x)图象上有且仅有一个最高点和一个最低点,且关于x的方程f(x)﹣a=0在区间[![]() ,
,![]() ]上有且仅有一解,求实数a的取值范围.
]上有且仅有一解,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E、F分别为AB、BC的中点,现在沿DE、DF及EF把△ADE、△CDF和△BEF折起,使A、B、C三点重合,重合后的点记为P.

问:(1)这个几何体是什么?
(2)这个几何体由几个面构成?每个面的三角形是什么三角形?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,![]() ,如图1.以
,如图1.以![]() 为折痕将
为折痕将![]() 折起,使点
折起,使点![]() 到达点
到达点![]() 的位置,如图2.
的位置,如图2.
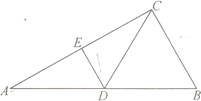

如图1 如图2
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值。
所成角的正弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列所给4个图象中,与所给3件事吻合最好的顺序为 ( )
(1)我离开家不久,发现自己把作业本忘在家里了,于是立刻返回家里取了作业本再上学;
(2)我出发后,心情轻松,缓缓行进,后来为了赶时间开始加速;
(3)我骑着车一路以常速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间.
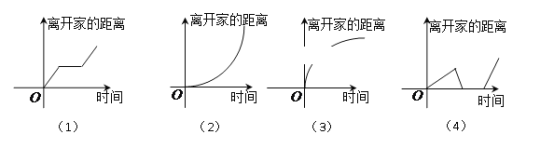
A. (1)(2)(4) B. (4)(2)(1) C. (4)(3)(1) D. (4)(1)(2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(10分)四面体ABCD及其三视图如图所示,平行于棱AD,BC的平面分别交四面体的棱AB,BD,DC,CA于点E,F,G,H.

(1)求四面体ABCD的体积;
(2)证明:四边形EFGH是矩形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汽车“定速巡航”技术是用于控制汽车的定速行驶,当汽车被设定为定速巡航状态时,电脑根据道路状况和汽车的行驶阻力自动控制供油量,使汽车始终保持在所设定的车速行驶,而无需司机操纵油门,从而减轻疲劳,促进安全,节省燃料.某汽车公司为测量某型号汽车定速巡航状态下的油耗情况,选择一段长度为240km的平坦高速路段进行测试.经多次测试得到一辆汽车每小时耗油量F(单位:L)与速度v(单位:km/h)(![]() )的下列数据:
)的下列数据:
v | 0 | 40 | 60 | 80 | 120 |
F | 0 |
|
| 10 | 20 |
为了描述汽车每小时耗油量与速度的关系,现有以下三种函数模型供选择:
![]() ,
, ,
,![]() .
.
(1)请选出你认为最符合实际的函数模型,并求出相应的函数解析式.
(2)这辆车在该测试路段上以什么速度行驶才能使总耗油量最少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com