练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图所示为一正方体的平面展开图，在这个正方体中，有下列四个命题：

    ①AF⊥GC；

    ②BD与GC成异面直线且夹角为60；

    ③BD∥MN；

    ④BG与平面ABCD所成的角为45.

    其中正确的个数是( )

    A. 1 B. 2 C. 3 D. 4

    【答案】B

    【解析】将平面展开图还原成正方体（如图所示）．

    对于①，由图形知AF与GC异面垂直，故①正确；

    对于②，BD与GC显然成异面直线．连EB，ED，则BM∥GC，所以即为异面直线BD与GC所成的角（或其补角）．在等边△BDM中， ，所以异面直线BD与GC所成的角为，故②正确；

    对于③，BD与MN为异面垂直，故③错误；

    对于④，由题意得GD⊥平面ABCD，所以∠GBD是BG与平面ABCD所成的角．但在Rt△BDG中，∠GBD不等于45 ，故④错误．

    综上可得①②正确．选B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，已知椭圆： 的离心率为，上、下顶点分别为、，点在椭圆上，且异于点、，直线、与直线： 分别交于点、，且面积的最大值为.

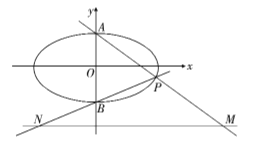
    （1）求椭圆的标准方程；

    （2）求线段的长的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 (m,n∈R)在x=1处取得极值2.

    (1)求f(x)的解析式；

    (2)k为何值时，方程f(x)-k=0只有1个根

    (3)设函数g(x)=x2-2ax+a，若对于任意x1∈R，总存在x2∈[-1,0]，使得g(x2)≤f(x1)，求a的取值范围

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】有一矩形硬纸板材料（厚度忽略不计），一边长为6分米，另一边足够长．现从中截取矩形（如图甲所示），再剪去图中阴影部分，用剩下的部分恰好能折卷成一个底面是弓形的柱体包装盒（如图乙所示，重叠部分忽略不计），其中是以为圆心、的扇形，且弧,分别与边, 相切于点, ．

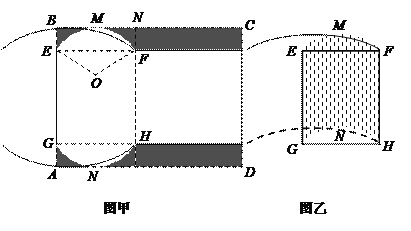
    （1）当长为1分米时，求折卷成的包装盒的容积；

    （2）当的长是多少分米时，折卷成的包装盒的容积最大？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】将圆上每个点的横坐标变为原来的4倍，纵坐标变为原来的3倍，得曲线，以坐标原点为极点， 轴的非负轴分别交于半轴为极轴建立极坐标系，直线的极坐标方程为： ，且直线在直角坐标系中与轴分别交于两点.

    （1）写出曲线的参数方程，直线的普通方程；

    （2）问在曲线上是否存在点，使得的面积，若存在，求出点的坐标，若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系xOy中，直线l经过点P(2,0)，其倾斜角为，在以原点O为极点，x轴非负半轴为极轴的极坐标系中（取相同的长度单位），曲线C的极坐标方程为．

    （Ⅰ）若直线l与曲线C有公共点，求倾斜角的取值范围；

    （Ⅱ）设M(x,y)为曲线C上任意一点，求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数是定义在上的偶函数.当时， .

    (1) 求曲线在点处的切线方程；

    (2) 若关于的不等式恒成立,求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知坐标平面上动点与两个定点， ，且.

    （1）求点的轨迹方程，并说明轨迹是什么图形；

    （2）记（1）中轨迹为，过点的直线被所截得的线段长度为8，求直线的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某花店每天以每枝5元的价格从农场购进若干枝玫瑰花，然后以每枝10元的价格出售，如果当天卖不完，剩下的玫瑰花作垃圾处理.

    （Ⅰ）若花店一天购进17枝玫瑰花，求当天的利润（单位：元）关于当天需求量（单位：枝， ）的函数解析式.

    （Ⅱ）花店记录了100天玫瑰花的日需求量（单位：枝），整理得下表：

    以100天记录的各需求量的频率作为各需求量发生的概率.

    （1）若花店一天购进17枝玫瑰花， 表示当天的利润（单位：元），求的分布列及数学期望；

    （2）若花店计划一天购进16枝或17枝玫瑰花，以利润角度看，你认为应购进16枝好还是17枝好？请说明理由.

    查看答案和解析>>

    同步练习册答案