Question

1．四棱锥P-ABCD的底面ABCD是直角梯形，AD∥BC，∠BAD=90°，侧面PAB⊥底面ABCD，△PAB为正三角形，AB=BC=$\frac{1}{2}$AD=2，E为PD中点
（1）求证：CE∥平面PAB；
（2）求二面角E-AC-D的余弦值；
（3）在线段BC上存在点Q使AQ⊥PD，求点Q到平面EAC的距离．

Answer 1

分析 解法一：（1）取AP中点F，连EF，BF，从而可证四边形EFBC为平行四边形，从而得到CE∥BF，从而证明CE∥平面PAB；
（2）作PG⊥AB于G，EH⊥DG于H，则EH∥PG，从而可知EH⊥底面ABCD过H；再作HM⊥AC于M，连EM，则EM⊥AC，∠EMH为二面角E-AC-D的平面角，从而求余弦值；
（3）由PG⊥底面ABCD，要使AQ⊥PD，只需要AQ⊥DG即可，利用体积相等求距离．
解法二：（向量法）建立空间直角坐标系O-xyz，从而得到点的坐标，从而写出可得$\overrightarrow{CE}$=$\overrightarrow{BM}$=（-$\frac{3}{2}$，0，$\frac{\sqrt{3}}{2}$），从而证明；
（2）设平面ACE的法向量$\overrightarrow{n}$=（x，y，1）；从而可得$\overrightarrow{n}$•$\overrightarrow{AC}$=2x+2y=0，$\overrightarrow{n}$•$\overrightarrow{AE}$=$\frac{1}{2}$x+2y+$\frac{\sqrt{3}}{2}$=0；从而求出$\overrightarrow{n}$=（$\frac{\sqrt{3}}{3}$，-$\frac{\sqrt{3}}{3}$，1）；从而求余弦值．

解答 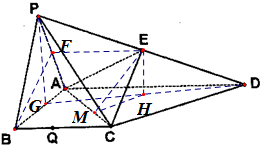解：解法一：（1）证明：取AP中点F，连EF，BF，
∵E为PD中点，∴EF∥AD且EF=$\frac{1}{2}$AD，
又∵BC∥AD且BC=$\frac{1}{2}$AD，∴EF∥BC且EF=BC，
∴四边形EFBC为平行四边形，
∴CE∥BF，
∴CE∥平面PAB；
（2）作PG⊥AB于G，EH⊥DG于H，则EH∥PG，
∵平面PAB⊥底面ABCD，
∴PG⊥底面ABCD，又EH∥PG，
∴EH⊥底面ABCD过H；
作HM⊥AC于M，连EM，则EM⊥AC，∠EMH为二面角E-AC-D的平面角，
可求得EH=$\frac{1}{2}$PG=$\frac{\sqrt{3}}{2}$，MH=CH•sin45°=$\frac{3}{2}$•$\frac{\sqrt{2}}{2}$=$\frac{3\sqrt{2}}{4}$；
∴tan∠EMH=$\frac{EH}{MH}$=$\frac{\sqrt{6}}{3}$，
∴二面角E-AC-D的余弦值为$\frac{\sqrt{15}}{5}$；
（3）∵PG⊥底面ABCD，要使AQ⊥PD，只需要AQ⊥DG即可．
在直角梯形ABCD中，由△ABQ∽△DAG，可得BQ=$\frac{1}{2}$，Q为BC的四等分点．
设Q到平面EAC的距离为h，可证BF⊥平面PAD，∵CE∥BF，∴△EAC为直角三形，
S_△EAC=$\frac{1}{2}$AE•CE=$\frac{1}{2}$•$\sqrt{5}$•$\sqrt{3}$=$\frac{\sqrt{15}}{2}$，
又S_△AQC=$\frac{1}{2}$×2×$\frac{3}{2}$=$\frac{3}{2}$，
由V_Q-EAC=V_E-AQC得，
h•S_△EAC=$\frac{\sqrt{3}}{2}$•S_△AQC，
∴h=$\frac{3\sqrt{5}}{10}$．
解法二：（向量法）如图建立这空间直角坐标系O-xyz，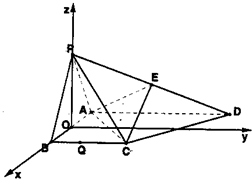

（1）容易得A（-1，0，0），C（1，2，0），B（1，0，0），P（0，0，$\sqrt{3}$），
D（-1，4，0），E（-$\frac{1}{2}$，2，$\frac{\sqrt{3}}{2}$）；
∴AP中点M（-$\frac{1}{2}$，0，$\frac{\sqrt{3}}{2}$），
可得$\overrightarrow{CE}$=$\overrightarrow{BM}$=（-$\frac{3}{2}$，0，$\frac{\sqrt{3}}{2}$），
∴CE∥BM；
∴CE∥平面PAB；
（2）设平面ACE的法向量$\overrightarrow{n}$=（x，y，1）；
$\overrightarrow{n}$•$\overrightarrow{AC}$=2x+2y=0，$\overrightarrow{n}$•$\overrightarrow{AE}$=$\frac{1}{2}$x+2y+$\frac{\sqrt{3}}{2}$=0；
解得：x=$\frac{\sqrt{3}}{3}$，y=-$\frac{\sqrt{3}}{3}$；
∴$\overrightarrow{n}$=（$\frac{\sqrt{3}}{3}$，-$\frac{\sqrt{3}}{3}$，1）；
设二面角E-AC-D的平面角为θ，
则cosθ=$\frac{|\overrightarrow{n}•\overrightarrow{OP}|}{|\overrightarrow{n}|•|\overrightarrow{OP}|}$=$\frac{\sqrt{15}}{5}$．

点评 本题考查了学生的空间想象力与空间向量的应用，同时考查了平面的证明与应用，属于难题．