
| A. | ①②③④ | B. | ②③ | C. | ②④ | D. | ③④ |
分析 根据双曲线,椭圆,抛物线的定义和性质,逐一分析四个结论的真假,可得答案.
解答 解:①设A、B为两个定点,k为非零常数,|OA|-|OB|=k>|AB|,则动点P的轨迹为双曲线
|OA|-|OB|=k=|AB|,则动点P的轨迹为两条射线,故错误;
②设定圆C上一定点A作圆的动弦AB,O为坐标原点,若$\overrightarrow{OP}$=$\frac{1}{2}$($\overrightarrow{OA}$+$\overrightarrow{OB}$),则P是AB的中点,
由AB的长度不变,则圆心C到AB的距离即CP长不变,
则动点P的轨迹为圆,故错误;
③抛物线y=$\frac{1}{8}$x2的标准方程为:x2=8y,故其焦点为(0,2)点,该点是椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$=1的上顶点,故正确;
④双曲线$\frac{{x}^{2}}{4}$-y2=-1的渐近线是$\frac{{x}^{2}}{4}$-y2=0,即y=±$\frac{1}{2}$x,故正确.
故选:D.
点评 本题以命题的真假判断为载体,考查了圆锥曲线的定义和性质,难度中档.


科目:高中数学 来源: 题型:选择题
| A. | 命题“若x2=1,则x=1”的否命题为:“若x2=1,则x≠1” | |
| B. | 命题“若一个数是负数,则它的平方是正数”的逆命题是“若一个数的平方不是正数,则它不是负数” | |
| C. | 命题“若x=y,则sinx=siny”的逆否命题为真命题 | |
| D. | 命题“?x∈R使得x2+x+1<0”的否定是:“?x∈R均有x2+x+1<0” |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A=R,B={x|x是正实数},f:A中的数的绝对值 | |
| B. | A={0,1},B={-1,0,1},f:A中的数的开方 | |
| C. | A=Z,B=Q,f:A中的数的倒数 | |
| D. | A={-1,0,1},B={-1,0,1},f:A中的数的平方 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,$\frac{3}{2}$) | B. | ($\frac{3}{2}$,3) | C. | (1,3) | D. | (2,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0∈R,${{x}_{0}}^{2}$≤lg1 | B. | ?x0∈R,${{x}_{0}}^{2}$<lg1 | ||
| C. | ?x∈R,${{x}_{0}}^{2}$≤lg1 | D. | $?{x_{\;}}∈R,x_{\;}^2<lg1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
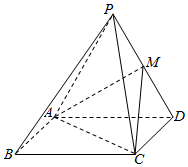 如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,且△PAD是边长为4的正三角形,M为PD的中点,底面ABCD是矩形,CD=3.
如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,且△PAD是边长为4的正三角形,M为PD的中点,底面ABCD是矩形,CD=3. 查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com