
| A. | 命题“若x2=1,则x=1”的否命题为:“若x2=1,则x≠1” | |
| B. | 命题“若一个数是负数,则它的平方是正数”的逆命题是“若一个数的平方不是正数,则它不是负数” | |
| C. | 命题“若x=y,则sinx=siny”的逆否命题为真命题 | |
| D. | 命题“?x∈R使得x2+x+1<0”的否定是:“?x∈R均有x2+x+1<0” |
分析 写出命题的否命题判断A;写出命题的逆命题判断B;由互为逆否命题的两个命题共真假判断C;直接写出特称命题的否定判断D.
解答 解:命题“若x2=1,则x=1”的否命题为:“若x2≠1,则x≠1”,故A错误;
命题“若一个数是负数,则它的平方是正数”的逆命题是“若一个数的平方是正数,则这个数是负数”,故B错误;
命题“若x=y,则sinx=siny”为真命题,故其逆否命题为真命题,C正确;
命题“?x∈R使得x2+x+1<0”的否定是:“?x∈R均有x2+x+1≥0”,故D错误.
故选:C.
点评 本题考查命题的真假判断与应用,考查了命题的逆命题、否命题以及逆否命题的真假判断,考查特称命题的否定,是基础题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 8 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | [-1,1) | C. | [-4,1) | D. | [-4,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
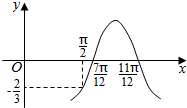 已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,0<φ<π)的部分图象如图所示,f($\frac{π}{2}$)=-$\frac{2}{3}$,f($\frac{7π}{12}$)=0,f($\frac{11π}{12}$)=0,则A=( )
已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,0<φ<π)的部分图象如图所示,f($\frac{π}{2}$)=-$\frac{2}{3}$,f($\frac{7π}{12}$)=0,f($\frac{11π}{12}$)=0,则A=( )| A. | 1 | B. | x | C. | 0 | D. | $\frac{2}{3}$$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①②③④ | B. | ②③ | C. | ②④ | D. | ③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com