
【题目】已知△ABC的内角A,B,C的对边分别为a,b,c.
(1)若![]() 的面积
的面积![]() ,求a+c值;
,求a+c值;
(2)若2cosC(![]() +
+![]() )=c2,求角C.
)=c2,求角C.
【答案】(1)5(2)![]()
【解析】
(1)由已知利用三角形面积公式可求ac=6,结合余弦定理可求a+c的值.
(2)利用平面向量数量积的运算,正弦定理,三角函数恒等变换的应用化简已知等式可求cosC=![]() ,结合范围C∈(0,π),可求C的值.
,结合范围C∈(0,π),可求C的值.
解:(1)∵![]() 的面积
的面积![]() ,
,
∴![]() =
=![]() acsinB=
acsinB=![]() ac,可得:ac=6,
ac,可得:ac=6,
∵由余弦定理b2=a2+c2-2accosB,可得:7=a2+c2-ac=(a+c)2-3ac=(a+c)2-18,
解得:a+c=5.
(2)∵2cosC(![]() +
+![]() )=c2,
)=c2,
∴2cosC(accosB+bccosA)=c2,可得:2cosC(acosB+bcosA)=c,
∴由正弦定理可得:2cosC(sinAcosB+sinBcosA)=sinC,即2cosCsinC=sinC,
∵sinC≠0,
∴cosC=![]() ,
,
∵C∈(0,π),
∴C=![]() .
.


 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:
【题目】已知函数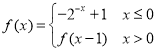 ,则下列命题中正确命题的个数是( )
,则下列命题中正确命题的个数是( )
①函数![]() 在
在![]() 上为周期函数
上为周期函数
②函数![]() 在区间
在区间![]() ,
,![]() 上单调递增
上单调递增
③函数![]() 在
在![]() (
(![]() )取到最大值
)取到最大值![]() ,且无最小值
,且无最小值
④若方程![]() (
(![]() )有且仅有两个不同的实根,则
)有且仅有两个不同的实根,则![]()
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知正三棱锥P-ABC的侧面是直角三角形,PA=6,顶点P在平面ABC内的正投影为点D,D在平面PAB内的正投影为点E,连结PE并延长交AB于点G.

(Ⅰ)证明:G是AB的中点;
(Ⅱ)在图中作出点E在平面PAC内的正投影F(说明作法及理由),并求四面体PDEF的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某学校研究性课题《什么样的活动最能促进同学们进行垃圾分类》向题的统计图(每个受访者都只能在问卷的5个活动中选择一个),以下结论错误的是( )

A. 回答该问卷的总人数不可能是100个
B. 回答该问卷的受访者中,选择“设置分类明确的垃圾桶”的人数最多
C. 回答该问卷的受访者中,选择“学校团委会宣传”的人数最少
D. 回答该问卷的受访者中,选择“公益广告”的人数比选择“学校要求”的少8个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 在椭圆
在椭圆![]() 上,
上,![]() 为坐标原点,直线
为坐标原点,直线![]() 的斜率与直线
的斜率与直线![]() 的斜率乘积为
的斜率乘积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)不经过点![]() 的直线
的直线![]() (
(![]() 且
且![]() )与椭圆
)与椭圆![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 关于原点的对称点为
关于原点的对称点为![]() (与点
(与点![]() 不重合),直线
不重合),直线![]() ,
,![]() 与
与![]() 轴分别交于两点
轴分别交于两点![]() ,
,![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
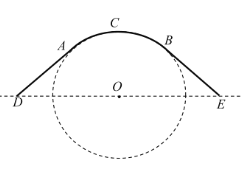
【题目】某公园为了美化环境和方便顾客,计划建造一座圆弧形拱桥,已知该桥的剖面如图所示,共包括圆弧形桥面![]() 和两条长度相等的直线型路面
和两条长度相等的直线型路面![]() 、
、![]() ,桥面跨度
,桥面跨度![]() 的长不超过
的长不超过![]() 米,拱桥
米,拱桥![]() 所在圆的半径为
所在圆的半径为![]() 米,圆心
米,圆心![]() 在水面
在水面![]() 上,且
上,且![]() 和
和![]() 所在直线与圆
所在直线与圆![]() 分别在连结点
分别在连结点![]() 和
和![]() 处相切.设
处相切.设![]() ,已知直线型桥面每米修建费用是
,已知直线型桥面每米修建费用是![]() 元,弧形桥面每米修建费用是
元,弧形桥面每米修建费用是![]() 元.
元.
(1)若桥面(线段![]() 、
、![]() 和弧
和弧![]() )的修建总费用为
)的修建总费用为![]() 元,求
元,求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)当![]() 为何值时,桥面修建总费用
为何值时,桥面修建总费用![]() 最低?
最低?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的质量以其质量指标值衡量,并依据质量指标值划分等级如下表:
![]()
从某企业生产的这种产品中抽取200件,检测后得到如下的频率分布直方图:
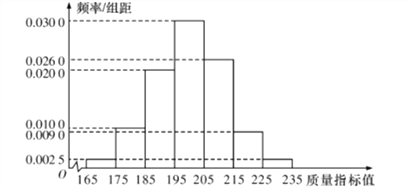
(1)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“一、二等品至少要占全部产品![]() ”的规定?
”的规定?
(2)在样本中,按产品等级用分层抽样的方法抽取8件,再从这8件产品中随机抽取4件,求抽取的4件产品中,一、二、三等品都有的概率;
(3)该企业为提高产品质量,开展了“质量提升月”活动,活动后再抽样检测,产品质量指标值![]() 近似满足
近似满足![]() ,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com