
【题目】已知点![]() 在椭圆
在椭圆![]() 上,
上,![]() 为坐标原点,直线
为坐标原点,直线![]() 的斜率与直线
的斜率与直线![]() 的斜率乘积为
的斜率乘积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)不经过点![]() 的直线
的直线![]() (
(![]() 且
且![]() )与椭圆
)与椭圆![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 关于原点的对称点为
关于原点的对称点为![]() (与点
(与点![]() 不重合),直线
不重合),直线![]() ,
,![]() 与
与![]() 轴分别交于两点
轴分别交于两点![]() ,
,![]() ,求证:
,求证:![]() .
.
【答案】(Ⅰ)![]() (Ⅱ)见解析
(Ⅱ)见解析
【解析】
(Ⅰ)根据椭圆的中点弦所在直线的斜率的性质,得到![]() ,得到
,得到![]() ,再结合椭圆所过的点的坐标满足椭圆方程,联立方程组,求得
,再结合椭圆所过的点的坐标满足椭圆方程,联立方程组,求得![]() ,进而求得椭圆的方程;
,进而求得椭圆的方程;
(Ⅱ)将直线方程与椭圆方程联立,消元,利用韦达定理得到两根和与两根积,将证明结果转化为证明直线![]() ,
,![]() 的斜率互为相反数,列式,可证.
的斜率互为相反数,列式,可证.
(Ⅰ)由题意,![]() ,
,
即![]() ① 又
① 又![]() ②
②
联立①①解得![]()
所以,椭圆![]() 的方程为:
的方程为:![]() .
.
(Ⅱ)设![]() ,
,![]() ,
,![]() ,由
,由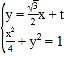 ,
,
得![]() ,
,
所以![]() ,即
,即![]() ,
,
又因为![]() ,所以,
,所以,![]() ,
,
![]() ,
,![]() ,
,
解法一:要证明![]() ,可转化为证明直线
,可转化为证明直线![]() ,
,![]() 的斜率互为相反数,只需证明
的斜率互为相反数,只需证明![]() ,即证明
,即证明![]() .
.
![]()
![]()
∴![]()
![]()
![]()
∴![]() ,∴
,∴![]() .
.
解法二:要证明![]() ,可转化为证明直线
,可转化为证明直线![]() ,
,![]() 与
与![]() 轴交点
轴交点![]() 、
、![]() 连线中点
连线中点![]() 的纵坐标为
的纵坐标为![]() ,即
,即![]() 垂直平分
垂直平分![]() 即可.
即可.
直线![]() 与
与![]() 的方程分别为:
的方程分别为:
![]() ,
,![]() ,
,
分别令![]() ,得
,得![]() ,
,![]()
而![]() ,同解法一,可得
,同解法一,可得![]()
![]() ,即
,即![]() 垂直平分
垂直平分![]() .
.
所以,![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设![]() 是平面上由
是平面上由![]() 个点组成的点集.若在
个点组成的点集.若在![]() 中任取四个点,均至少有一个点与其余三个点相连,则下面结论中正确的是______.
中任取四个点,均至少有一个点与其余三个点相连,则下面结论中正确的是______.
①![]() 中不存在与其他所有点相连的点;
中不存在与其他所有点相连的点;
②![]() 中至少有一个点与其余所有的点均相连;
中至少有一个点与其余所有的点均相连;
③![]() 中至多有两个点与其余的点不相连;
中至多有两个点与其余的点不相连;
④![]() 中至多有两个点与其余所有的点均相连.
中至多有两个点与其余所有的点均相连.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体![]() 中,点
中,点![]() 在线段
在线段![]() 上运动,则下列判断中正确的是( )
上运动,则下列判断中正确的是( )

①平面![]() 平面
平面![]() ;
;
②![]() 平面
平面![]() ;
;
③异面直线![]() 与
与![]() 所成角的取值范围是
所成角的取值范围是![]() ;
;
④三棱锥![]() 的体积不变.
的体积不变.
A. ①② B. ①②④ C. ③④ D. ①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子中有大小、形状完全相同的四个小球,分别写有和、“谐”、“校”“园”四个字,有放回地从中任意摸出一个小球,直到“和”、“谐”两个字都摸到就停止摸球,用随机模拟的方法估计恰好在第三次停止摸球的概率。利用电脑随机产生![]() 到
到![]() 之间取整数值的随机数,分别用
之间取整数值的随机数,分别用![]() ,
,![]() ,
,![]() ,
,![]() 代表“和”、“谐”、“校”、“园”这四个字,以每三个随机数为一组,表示摸球三次的结果,经随机模拟产生了以下
代表“和”、“谐”、“校”、“园”这四个字,以每三个随机数为一组,表示摸球三次的结果,经随机模拟产生了以下![]() 组随机数:
组随机数:
![]()
由此可以估计,恰好第三次就停止摸球的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人轮流吹同一只气球,当且仅当气球内的气体体积![]() (单位:毫升)大于2014时,气球会被吹破.先由甲开始吹入1毫升气体,约定以后每次吹入的气体体积为上一次体积的2倍或
(单位:毫升)大于2014时,气球会被吹破.先由甲开始吹入1毫升气体,约定以后每次吹入的气体体积为上一次体积的2倍或![]() ,且吹入的气体体积为整数.
,且吹入的气体体积为整数.
(1)若谁先吹破气球谁输,问谁有必胜策略?证明你的结论.
(2)若在不吹破气球的前提下,约定单次吹入的气体体积最大者为赢家(如果吹入的体积相同,则最先吹出最大体积者为赢家).问:谁有必胜策略?证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com