
【题目】如图,在正方体![]() 中,点
中,点![]() 在线段
在线段![]() 上运动,则下列判断中正确的是( )
上运动,则下列判断中正确的是( )

①平面![]() 平面
平面![]() ;
;
②![]() 平面
平面![]() ;
;
③异面直线![]() 与
与![]() 所成角的取值范围是
所成角的取值范围是![]() ;
;
④三棱锥![]() 的体积不变.
的体积不变.
A. ①② B. ①②④ C. ③④ D. ①④
【答案】B
【解析】
①连接DB1,容易证明DB1⊥面ACD1 ,从而可以证明面面垂直;
②连接A1B,A1C1容易证明平面BA1C1∥面ACD1,从而由线面平行的定义可得;
③分析出A1P与AD1所成角的范围,从而可以判断真假;
④![]() =
=![]() ,C到面 AD1P的距离不变,且三角形AD1P的面积不变;
,C到面 AD1P的距离不变,且三角形AD1P的面积不变;
对于①,连接DB1,根据正方体的性质,有DB1⊥面ACD1 ,DB1平面PB1D,从而可以证明平面PB1D⊥平面ACD1,正确.
②连接A1B,A1C1容易证明平面BA1C1∥面ACD1,从而由线面平行的定义可得 A1P∥平面ACD1,正确.
③当P与线段BC1的两端点重合时,A1P与AD1所成角取最小值![]() ,
,
当P与线段BC1的中点重合时,A1P与AD1所成角取最大值![]() ,
,
故A1P与AD1所成角的范围是![]() ,错误;
,错误;
④![]() =
=![]() ,C到面AD1P的距离不变,且三角形AD1P的面积不变.
,C到面AD1P的距离不变,且三角形AD1P的面积不变.
∴三棱锥A﹣D1PC的体积不变,正确;
正确的命题为①②④.
故选:B.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域为[-1,5],部分对应值如下表,
的定义域为[-1,5],部分对应值如下表,![]() 的导函数
的导函数![]() 的图象如图所示,下列关于
的图象如图所示,下列关于![]() 的命题正确的是( )
的命题正确的是( )
|
| 0 | 4 | 5 |
| 1 | 2 | 2 | 1 |
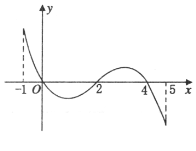
A.函数![]() 的极大值点为0,4;
的极大值点为0,4;
B.函数![]() 在[0,2]上是减函数;
在[0,2]上是减函数;
C.如果当![]() 时,
时,![]() 的最大值是2,那么
的最大值是2,那么![]() 的最大值为4;
的最大值为4;
D.函数![]() 的零点个数可能为0、1、2、3、4个.
的零点个数可能为0、1、2、3、4个.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两队进行篮球决赛,采取五场三胜制(当一队赢得三场胜利时,该队获胜,比赛结束).根据前期比赛成绩,甲队的主客场安排依次为“主主客客主”.设甲队主场取胜的概率为![]() ,客场取胜的概率为
,客场取胜的概率为![]() ,且各场比赛结果相互独立,则甲队不超过
,且各场比赛结果相互独立,则甲队不超过![]() 场即获胜的概率是( )
场即获胜的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高二年级共有800名学生参加了数学测验(满分150分),已知这800名学生的数学成绩均不低于90分,将这800名学生的数学成绩分组如:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到的频率分布直方图如图所示,则下列说法中正确的是( )
,得到的频率分布直方图如图所示,则下列说法中正确的是( )
①![]() ;②这800名学生中数学成绩在110分以下的人数为160; ③这800名学生数学成绩的中位数约为121.4;④这800名学生数学成绩的平均数为125.
;②这800名学生中数学成绩在110分以下的人数为160; ③这800名学生数学成绩的中位数约为121.4;④这800名学生数学成绩的平均数为125.
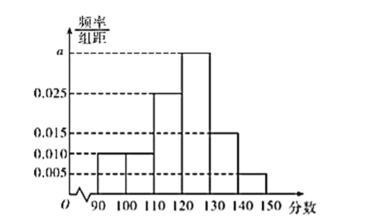
A.①②B.②③C.②④D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 在椭圆
在椭圆![]() 上,
上,![]() 为坐标原点,直线
为坐标原点,直线![]() 的斜率与直线
的斜率与直线![]() 的斜率乘积为
的斜率乘积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)不经过点![]() 的直线
的直线![]() (
(![]() 且
且![]() )与椭圆
)与椭圆![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 关于原点的对称点为
关于原点的对称点为![]() (与点
(与点![]() 不重合),直线
不重合),直线![]() ,
,![]() 与
与![]() 轴分别交于两点
轴分别交于两点![]() ,
,![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:
①“三个球全部放入两个盒子,其中必有一个盒子有一个以上的球”是必然事件
②“当![]() 为某一实数时可使
为某一实数时可使![]() ”是不可能事件
”是不可能事件
③“明天全天要下雨”是必然事件
④“从100个灯泡(6个是次品)中取出5个,5个都是次品”是随机事件.
其中正确命题的个数是( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为响应“文化强国建设”号召,并增加学生们对古典文学的学习兴趣,雅礼中学计划建设一个古典文学熏陶室.为了解学生阅读需求,随机抽取200名学生做统计调查.统计显示,男生喜欢阅读古典文学的有64人,不喜欢的有56人;女生喜欢阅读古典文学的有36人,不喜欢的有44人.
(1)能否在犯错误的概率不超过0.25的前提下认为喜欢阅读古典文学与性别有关系?
(2)为引导学生积极参与阅读古典文学书籍,语文教研组计划牵头举办雅礼教育集团古典文学阅读交流会.经过综合考虑与对比,语文教研组已经从这200人中筛选出了5名男生代表和4名女生代表,其中有3名男生代表和2名女生代表喜欢古典文学.现从这9名代表中任选3名男生代表和2名女生代表参加交流会,记![]() 为参加交流会的5人中喜欢古典文学的人数,求
为参加交流会的5人中喜欢古典文学的人数,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
附: ,其中
,其中![]() .
.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com