【题目】在
名学生中，已知任意三人中有两人互相认识，任意四人中有两人互相不认识，则的最大值为______.
七星图书口算速算天天练系列答案
初中学业考试导与练系列答案科目：高中数学 来源： 题型：
【题目】如图所示的折线图为某小区小型超市今年1月份到5月份的营业额和支出数据（利润=营业额－支出），根据折线图，下列说法正确的是（ ）
A.该超市这五个月中的营业额一直在增长；
B.该超市这五个月的利润一直在增长；
C.该超市这五个月中五月份的利润最高；
D.该超市这五个月中的营业额和支出呈正相关．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在某亲子游戏结束时有一项抽奖活动，抽奖规则是：盒子里面共有4个小球，小球上分别写有0，1，2，3的数字，小球除数字外其他完全相同，每对亲子中，家长先从盒子中取出一个小球，记下数字后将小球放回，孩子再从盒子中取出一个小球，记下小球上数字将小球放回．抽奖活动的奖励规则是：①若取出的两个小球上数字之积大于4，则奖励飞机玩具一个；②若取出的两个小球上数字之积在区间上
，则奖励汽车玩具一个；③若取出的两个小球上数字之积小于1，则奖励饮料一瓶．
（1）求每对亲子获得飞机玩具的概率；
（2）试比较每对亲子获得汽车玩具与获得饮料的概率，哪个更大？请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，有一块半径为20米，圆心角
的扇形展示台，展示台分成了四个区域：三角形
，弓形
，扇形
和扇形
（其中
）.某次菊花展依次在这四个区域摆放：泥金香、紫龙卧雪、朱砂红霜、朱砂红霜.预计这三种菊花展示带来的日效益分别是：泥金香50元/米
，紫龙卧雪30元/米，朱砂红霜40元/米.
（1）设
，试建立日效益总量
关于
的函数关系式；
（2）试探求为何值时，日效益总量达到最大值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某校高二年级共有800名学生参加了数学测验（满分150分），已知这800名学生的数学成绩均不低于90分，将这800名学生的数学成绩分组如：
，
，
，
，
，得到的频率分布直方图如图所示，则下列说法中正确的是( )
①
；②这800名学生中数学成绩在110分以下的人数为160； ③这800名学生数学成绩的中位数约为121.4；④这800名学生数学成绩的平均数为125.
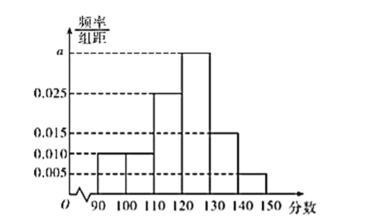
A.①②B.②③C.②④D.③④
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】假设今天是4月23日，某市未来六天的空气质量预报情况如下图所示.该市有甲、乙、丙三人计划在未来六天（4月24日～4月29日）内选择一天出游，甲只选择空气质量为优的一天出游，乙不选择周一出游，丙不选择明天出游，且甲与乙不选择同一天出游，则这三人出游的不同方法数为________.
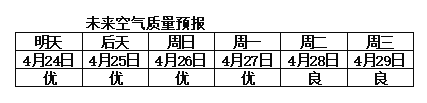
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知点
在椭圆
上，
为坐标原点，直线
的斜率与直线
的斜率乘积为
.
（1）求椭圆
的方程；
（2）不经过点
的直线
（
且
）与椭圆交于
，
两点，关于原点的对称点为
（与点不重合），直线
，
与
轴分别交于两点
，
，求证：
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】[选修4-4：坐标系与参数方程]
已知曲线
的极坐标方程为
，以极点
为直角坐标原点，以极轴为
轴的正半轴建立平面直角坐标系
，将曲线向左平移
个单位长度，再将得到的曲线上的每一个点的横坐标缩短为原来的
，纵坐标保持不变，得到曲线
（1）求曲线的直角坐标方程；
（2）已知直线
的参数方程为
，（
为参数），点
为曲线上的动点，求点到直线距离的最大值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】等腰直角△
内接于抛物线
(
)，其中
为抛物线的顶点，
，△的面积是16.
（1）求抛物线
的方程；
（2）抛物线的焦点为
，过的直线交抛物线于
两点，交
轴于点
，若
，
，证明：
是一个定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
