
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 逐项判断即可.4个命题都可以利用作差法比较大小,从而得到答案.
解答 解:①$a+\frac{1}{b}-b-\frac{1}{a}=a-b+\frac{a-b}{ab}$=$(a-b)(1+\frac{1}{ab})$,∵a>b>0,∴$(a-b)(1+\frac{1}{ab})>0$,故①正确;
②由ac2>bc2可知c2>0,所以a>b,故②正确;
③$\frac{a}{b}-\frac{a+1}{b+1}=\frac{a-b}{b(b+1)}$因为a>b>0,所以$\frac{a-b}{b(b+1)}$>0,故③错误;
④由$\frac{1}{a}>\frac{1}{b}$有$\frac{1}{a}-\frac{1}{b}=\frac{b-a}{ab}$>0,又a>b,所以ab<0,所以b<0,a>0,故④正确.
综上可知正确的命题为①②④.
故选:C.
点评 本题考查不等式比较大小.能利用作差比较法比较是解题关键.基础题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
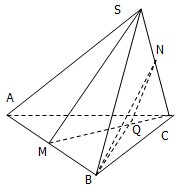 如图所示,已知S是边长为1的正三角形所在平面外一点,且SA=SB=SC=1,M,N分别是AB,SC的中点,求异面直线SM与BN所成角的余弦值.
如图所示,已知S是边长为1的正三角形所在平面外一点,且SA=SB=SC=1,M,N分别是AB,SC的中点,求异面直线SM与BN所成角的余弦值.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{4}{5}$ | C. | $\frac{7}{8}$ | D. | $\frac{6}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{7}$ | C. | $\frac{1}{87}$ | D. | $\frac{1}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 直角三角形 | B. | 等腰三角形 | ||
| C. | 等腰直角三角形 | D. | 等腰或直角三角形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com