
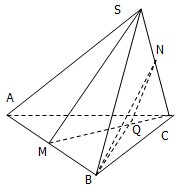
 如图所示,已知S是边长为1的正三角形所在平面外一点,且SA=SB=SC=1,M,N分别是AB,SC的中点,求异面直线SM与BN所成角的余弦值.
如图所示,已知S是边长为1的正三角形所在平面外一点,且SA=SB=SC=1,M,N分别是AB,SC的中点,求异面直线SM与BN所成角的余弦值. 分析 连接CM,过N作NQ∥SM,并连接BQ,根据中位线的性质,直角三角形边的关系以及余弦定理表示出BN,NQ,BQ,并根据余弦定理求出cos∠BNQ,从而求得∠BNQ,并根据∠BNQ的大小判断该角是否是异面直线SM,BN所成的角,并求出这个角.
解答 解:如图,连接CM,过N作SM的平行线NQ,交CM与Q,连接BQ;
则SM=$\frac{\sqrt{3}}{2}$,NQ=$\frac{\sqrt{3}}{4}$;BQ=$\frac{\sqrt{7}}{4}$,BN=$\frac{\sqrt{3}}{2}$
∴cos∠BNQ=$\frac{\frac{3}{16}+\frac{3}{4}-\frac{7}{16}}{2×\frac{\sqrt{3}}{4}×\frac{\sqrt{3}}{2}}$=$\frac{1}{3}$,
∵NQ∥SM,∴∠BNQ是异面直线SM与BN的所成角余弦值为$\frac{1}{3}$.
点评 考查三角形中位线的性质,余弦定理,异面直线所成的角的概念及求法.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 164石 | B. | 178石 | C. | 189石 | D. | 196石 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com