
分析 (1)确定集合A,(∁UA)∩B=∅,根据集合的基本运算即可求m的值;
(2)根据B⊆A,建立条件关系即可求实数n的取值范围.
解答 解:(1)∵U=R,集合A={x|x2+3x+2=0}={-2,-1},B={x|x2+(m+1)x+m=0}={x|(x+1)(x+m)=0};
(CUA)∩B=ϕ,
可得:B⊆A,
当m=1时,则B={-1},符合B⊆A;
当m≠1时,则B={-1,-m},
∵B⊆A,
∴-m=-2,即m=2,
故得实数m为1或2.
(2)集合A={x|-2≤x≤5},B={x|n+1≤x≤2n-1},
∵B⊆A,
∴有:$\left\{\begin{array}{l}{n+1≥-2}\\{2n-1≤5}\\{n+1≤2n-1}\end{array}\right.$,
解得:2≤n≤3.
故得实数n的取值范围是[2,3].
点评 本题考查了集合的化简与运算,属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{2}{3}$ | C. | 4 | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①用简单随机抽样法,②用系统抽样法 | |
| B. | ①用分层抽样法,②用简单随机抽样法 | |
| C. | ①用系统抽样法,②用分层抽样法 | |
| D. | ①用分层抽样法,②用系统抽样法 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
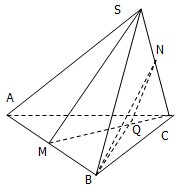 如图所示,已知S是边长为1的正三角形所在平面外一点,且SA=SB=SC=1,M,N分别是AB,SC的中点,求异面直线SM与BN所成角的余弦值.
如图所示,已知S是边长为1的正三角形所在平面外一点,且SA=SB=SC=1,M,N分别是AB,SC的中点,求异面直线SM与BN所成角的余弦值.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com