
分析 (1)结合三角恒等变换得到f(x)=sin(2x-$\frac{π}{3}$),由正弦函数图象的性质来求其单调增区间.
(2)运用向量等式得到D为三角形的重心,以AB、AC为邻边作平行四边形ABEC,通过解三角形解答.
解答 解:(1)由题可知f(x)=$\frac{1}{2}$sin2x-$\frac{\sqrt{3}}{2}$(1+cosx)+$\frac{\sqrt{3}}{2}$=sin(2x-$\frac{π}{3}$),
令2kπ$-\frac{π}{2}$≤2x-$\frac{π}{3}$≤2kπ+$\frac{π}{2}$,k∈Z.
则kπ-$\frac{π}{12}$≤x≤kπ+$\frac{5π}{12}$,k∈Z.
即函数f(x)的单调递增区间为[kπ-$\frac{π}{12}$,kπ+$\frac{5π}{12}$],k∈Z.
(2)由f(A)=$\frac{\sqrt{3}}{2}$,所以sin(2A-$\frac{π}{3}$)=$\frac{\sqrt{3}}{2}$,
解得A=$\frac{π}{3}$或A=$\frac{π}{2}$(舍).
又∵$\overrightarrow{AB}$+$\overrightarrow{AC}$=3$\overrightarrow{AD}$,
∴D为△ABC的重心,以AB、AC为邻边作平行四边形ABEC,
∵AD=2,
∴AE=6,
在△ABE中,AB=$\sqrt{3}$,∠ABE=120°,
由正弦定理可得$\frac{\sqrt{3}}{sin∠AEB}$=$\frac{6}{\frac{\sqrt{3}}{2}}$,
解得sin∠AEB=$\frac{1}{4}$且cos∠AEB=$\frac{\sqrt{15}}{4}$.
因此sin∠BAD=sin∠($\frac{π}{3}$-∠AEB)=$\frac{\sqrt{3}}{2}$×$\frac{\sqrt{15}}{4}$-$\frac{1}{2}$×$\frac{1}{4}$=$\frac{3\sqrt{5}-1}{8}$.
点评 本题考查三角函数的化简以及恒等变换公式的应用,还有解三角形的内容,如正弦定理等.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①用简单随机抽样法,②用系统抽样法 | |
| B. | ①用分层抽样法,②用简单随机抽样法 | |
| C. | ①用系统抽样法,②用分层抽样法 | |
| D. | ①用分层抽样法,②用系统抽样法 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -14 | B. | -9 | C. | -5 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
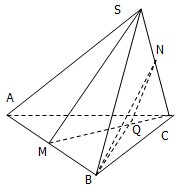 如图所示,已知S是边长为1的正三角形所在平面外一点,且SA=SB=SC=1,M,N分别是AB,SC的中点,求异面直线SM与BN所成角的余弦值.
如图所示,已知S是边长为1的正三角形所在平面外一点,且SA=SB=SC=1,M,N分别是AB,SC的中点,求异面直线SM与BN所成角的余弦值.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 社团 | 围棋 | 戏剧 | 足球 |
| 人数 | 10 | m | n |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{4}{5}$ | C. | $\frac{7}{8}$ | D. | $\frac{6}{7}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com