
【题目】
设函数f(x)=alnx﹣bx2(x>0).
(1)若函数f(x)在x=1处于直线![]() 相切,求函数f(x)在
相切,求函数f(x)在![]() 上的最大值;
上的最大值;
(2)当b=0时,若不等式f(x)≥m+x对所有的a∈[1,![]() ],x∈[1,e2]都成立,求实数m的取值范围.
],x∈[1,e2]都成立,求实数m的取值范围.
【答案】(Ⅰ)![]() ;(Ⅱ)(﹣∞,2﹣e2].
;(Ⅱ)(﹣∞,2﹣e2].
【解析】试题分析:(1)对函数求导,利用函数在![]() 处与
处与![]() 相切,可得关于
相切,可得关于![]() 方程,求出
方程,求出![]() ,再利用导函数判断函数在
,再利用导函数判断函数在![]() 上的单调性,结合单调性求得函数最大值.(Ⅱ)用分离变量法,将原问题转化为
上的单调性,结合单调性求得函数最大值.(Ⅱ)用分离变量法,将原问题转化为![]() ,对所有的
,对所有的![]() ,构造函数
,构造函数![]() 利用一次函数单调性,求出最小值
利用一次函数单调性,求出最小值![]() ,再进一步利用函数单调性,求出最小值后可得
,再进一步利用函数单调性,求出最小值后可得![]() 的范围.
的范围.
试题解析:(Ⅰ)∵f′(x)=![]() ﹣2bx,
﹣2bx,
又函数f(x)在x=1处与直线y=﹣![]() 相切,
相切,
∴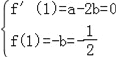 ,解得
,解得![]() .
.
f(x)=lnx﹣![]() x2,f′(x)=
x2,f′(x)=![]() ﹣x=﹣
﹣x=﹣![]() ,
,
当x∈[![]() ,1),f′(x)<0,f(x)递增,
,1),f′(x)<0,f(x)递增,
当x∈(1,e],f′(x)>0,f(x)递减.
即有f(x)的最大值为f(1)=﹣![]() ;
;
(Ⅱ)当b=0时,f(x)=alnx,
若不等式f(x)≥m+x对所有的a∈[1,![]() ],x∈[1,e2]都成立,
],x∈[1,e2]都成立,
即m≤alnx﹣x对所有的a∈[1,![]() ],x∈[1,e2]都成立,
],x∈[1,e2]都成立,
令h(a)=alnx﹣x,则h(a)为一次函数,
∴m≤h(a)min.
∵x∈[1,e2],∴lnx≥0,
∴h(a)在[1,![]() ]上单调递增,
]上单调递增,
∴h(a)min=h(1)=lnx﹣x,
∴m≤lnx﹣x对所有的x∈(1,e2]都成立.
由y=lnx﹣x(1<x≤e2)的导数为y′=![]() ﹣1<0,
﹣1<0,
则函数y=lnx﹣x(1<x≤e2)递减,
∵1<x≤e2,∴lnx﹣x≥2﹣e2,
则m≤2﹣e2.
则实数m的取值范围为(﹣∞,2﹣e2]


科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点
的焦点![]() 也是椭圆
也是椭圆![]() 的一个焦点,
的一个焦点,![]() 与
与![]() 的公共弦的长为
的公共弦的长为![]() .
.
(1)求![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 与
与![]() 相交于
相交于![]() ,
,![]() 两点,与
两点,与![]() 相交于
相交于![]() ,
,![]() 两点,且
两点,且![]() 与
与![]() 同向
同向
(ⅰ)若![]() ,求直线
,求直线![]() 的斜率
的斜率
(ⅱ)设![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴的交点为
轴的交点为![]() ,证明:直线
,证明:直线![]() 绕点
绕点![]() 旋转时,
旋转时,![]() 总是钝角三角形
总是钝角三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在原点,焦点在
的中心在原点,焦点在![]() 轴上,离心率
轴上,离心率![]() .以两个焦点和短轴的两个端点为顶点的四边形的周长为8,面积为
.以两个焦点和短轴的两个端点为顶点的四边形的周长为8,面积为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若点![]() 为椭圆
为椭圆![]() 上一点,直线
上一点,直线![]() 的方程为
的方程为![]() ,求证:直线
,求证:直线![]() 与椭圆
与椭圆![]() 有且只有一个交点.
有且只有一个交点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的一块木料中,棱BC平行于面A′C′.
(Ⅰ)要经过面A′C′内的一点P和棱BC将木料锯开,应怎样画线?
(Ⅱ)所画的线与平面AC是什么位置关系?并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知单调递增的等比数列{an}满足:a2+a3+a4=28,且a3+2是a2 , a4的等差中项.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=anlog ![]() an , 求数列{bn}的前n项和Sn .
an , 求数列{bn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4 坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为 (
( ![]() 为参数).以原点为极点,
为参数).以原点为极点, ![]() 轴正半轴为极轴 建立极坐标系,圆
轴正半轴为极轴 建立极坐标系,圆![]() 的方程为
的方程为![]() .
.
(1)写出直线![]() 的普通方程和圆
的普通方程和圆![]() 的直角坐标方程;
的直角坐标方程;
(2)若点![]() 的直角坐标为
的直角坐标为![]() ,圆
,圆![]() 与直线
与直线![]() 交于A,B两点,求
交于A,B两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦点在
的焦点在![]() 轴上,且椭圆
轴上,且椭圆![]() 的焦距为2.
的焦距为2.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于两点
交于两点![]() ,过
,过![]() 作
作![]() 轴且与椭圆
轴且与椭圆![]() 交于另一点
交于另一点![]() ,
, ![]() 为椭圆
为椭圆![]() 的右焦点,求证:三点
的右焦点,求证:三点![]() 在同一条直线上.
在同一条直线上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有800名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩进行统计. 请你根据尚未完成并有局部污损的频率分布表和频率分布直方图,解答下列问题:
分组 | 频数 | 频率 |
50.5~60.5 | 6 | 0.08 |
60.5~70.5 | 0.16 | |
70.5~80.5 | 15 | |
80.5~90.5 | 24 | 0.32 |
90.5~100.5 | ||
合计 | 75 | 1.00 |
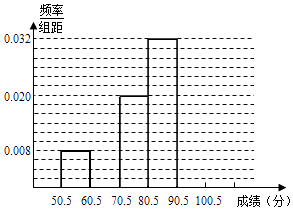
(1)填充频率分布表的空格;
(2)补全频率分布直方图;
(3)根据频率分布直方图求此次“环保知识竞赛”的平均分为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一组数据的平均数是2.8,方差是3.6,若将这组数据中的每一个数据都加上60,得到一组新数据,则所得新数据的平均数和方差分别是( )
A.57.2,3.6
B.57.2,56.4
C.62.8,63.6
D.62.8,3.6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com