
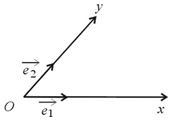
 如图,设ox,oy是平面内相交成θ°的两条数轴,$\overrightarrow{e_1}$,$\overrightarrow{e_2}$分别是与ox,oy正方向同向的单位向量,若向量$\overrightarrow{op}=x\overrightarrow{e_1}+y\overrightarrow{e_2}$,则把有序实数对(x,y)叫做向量$\overrightarrow{op}$的θ°坐标,记作$\overrightarrow{op}$(θ°)=(x,y);当θ=90°时,称(x,y)为$\overrightarrow{op}$的正交坐标.
如图,设ox,oy是平面内相交成θ°的两条数轴,$\overrightarrow{e_1}$,$\overrightarrow{e_2}$分别是与ox,oy正方向同向的单位向量,若向量$\overrightarrow{op}=x\overrightarrow{e_1}+y\overrightarrow{e_2}$,则把有序实数对(x,y)叫做向量$\overrightarrow{op}$的θ°坐标,记作$\overrightarrow{op}$(θ°)=(x,y);当θ=90°时,称(x,y)为$\overrightarrow{op}$的正交坐标.分析 (1)由向量的 θ0坐标定义得$\overrightarrow{OP}=-2\overrightarrow{{e}_{1}}+2\sqrt{2}\overrightarrow{{e}_{2}}$,且$\overrightarrow{{e}_{1}}$与$\overrightarrow{{e}_{2}}$的夹角为45°,由此能求出|$\overrightarrow{OP}$|.
(2)设与$\overrightarrow{{e}_{1}}$成600的单位向量为$\overrightarrow{{e}_{2}}$,与$\overrightarrow{{e}_{1}}$成900的单位向量为$\overrightarrow{{e}_{3}}$,则$\overrightarrow{{e}_{3}}$⊥$\overrightarrow{{e}_{1}}$,且$\overrightarrow{{e}_{3}}$与$\overrightarrow{{e}_{2}}$成300角,令$\overrightarrow{{e}_{3}}$(600)=(x,y),则$\overrightarrow{{e}_{3}}$=x$\overrightarrow{{e}_{1}}$+y$\overrightarrow{{e}_{2}}$.再由$\overrightarrow{{e}_{1}}$•$\overrightarrow{{e}_{3}}$=0,cos30°=$\overrightarrow{{e}_{2}}•\overrightarrow{{e}_{3}}$,能求出$\overrightarrow{OM}$(60°).
解答 解:(1)由向量的 θ0坐标定义得$\overrightarrow{OP}=-2\overrightarrow{{e}_{1}}+2\sqrt{2}\overrightarrow{{e}_{2}}$,
且$\overrightarrow{{e}_{1}}$与$\overrightarrow{{e}_{2}}$的夹角为45°,
∴|$\overrightarrow{OP}$|=$\sqrt{{\overrightarrow{OP}}^{2}}$=$\sqrt{4{\overrightarrow{{e}_{1}}}^{2}+2(-2\overrightarrow{{e}_{1}})•(2\sqrt{2}\overrightarrow{{e}_{2}})+8{\overrightarrow{{e}_{2}}}^{2}}$=2.
(2)设与$\overrightarrow{{e}_{1}}$成600的单位向量为$\overrightarrow{{e}_{2}}$,与$\overrightarrow{{e}_{1}}$成900的单位向量为$\overrightarrow{{e}_{3}}$,
则$\overrightarrow{{e}_{3}}$⊥$\overrightarrow{{e}_{1}}$,且$\overrightarrow{{e}_{3}}$与$\overrightarrow{{e}_{2}}$成300角,
令$\overrightarrow{{e}_{3}}$(600)=(x,y),则$\overrightarrow{{e}_{3}}$=x$\overrightarrow{{e}_{1}}$+y$\overrightarrow{{e}_{2}}$.
又$\overrightarrow{{e}_{1}}$•$\overrightarrow{{e}_{3}}$=0,cos30°=$\overrightarrow{{e}_{2}}•\overrightarrow{{e}_{3}}$,
即$\overrightarrow{{e}_{1}}$•($x\overrightarrow{{e}_{1}}+y\overrightarrow{{e}_{2}}$)=0,$\frac{\sqrt{3}}{2}=\overrightarrow{{e}_{2}}•(x\overrightarrow{{e}_{1}}+y\overrightarrow{{e}_{2}})$,
所以 $\left\{{\begin{array}{l}{x+\frac{1}{2}y=0}\\{\frac{1}{2}x+y=\frac{{\sqrt{3}}}{2}}\end{array}}\right.$解得 x=-$\frac{{\sqrt{3}}}{3}$,y=$\frac{{2\sqrt{3}}}{3}$
则$\overrightarrow{{e}_{3}}$=-$\frac{\sqrt{3}}{3}$$\overrightarrow{{e}_{1}}$+$\frac{2\sqrt{3}}{3}\overrightarrow{{e}_{2}}$.
∴$\overrightarrow{OM}$=2$\overrightarrow{{e}_{1}}$+$\sqrt{3}$$\overrightarrow{{e}_{3}}$=2$\overrightarrow{{e}_{1}}$+$\sqrt{3}$(-$\frac{{\sqrt{3}}}{3}$$\overrightarrow{{e}_{1}}+\frac{2\sqrt{3}}{3}\overrightarrow{{e}_{2}}$)=$\overrightarrow{{e}_{1}}+2\overrightarrow{{e}_{2}}$,
故$\overrightarrow{OM}$(60°)=(1,2).
点评 本题考查θ°坐标、正交坐标、向量等基础知识,考查推理论证能力、运算求解能力,考查数形结合思想、函数与方程思想,是中档题.


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:高中数学 来源: 题型:选择题
| A. | △ABC的内部 | B. | △ABC的外部 | C. | P在线段AC上 | D. | P在线段AB上 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | $-\frac{3}{2}$ | C. | -2 | D. | -6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若ac>bc,则a>b | B. | 若a2>b2,则a>b | ||
| C. | 若a>b,c<0,则a+c<b+c | D. | 若$\sqrt{a}$<$\sqrt{b}$,则a<b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}\overrightarrow b+\frac{1}{3}\overrightarrow c$ | B. | $\frac{1}{3}\overrightarrow b+\frac{2}{3}\overrightarrow c$ | C. | $\frac{2}{3}$$\overrightarrow{b}$-$\frac{1}{3}$$\overrightarrow{c}$ | D. | $\frac{1}{3}\overrightarrow b-\frac{2}{3}\overrightarrow c$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com