
【题目】已知函数![]() .
.
(![]() )若曲线
)若曲线![]() 与直线
与直线![]() 相切于点
相切于点![]() ,求点
,求点![]() 的坐标.
的坐标.
(![]() )令
)令![]() ,当
,当![]() 时,求
时,求![]() 的单调区间.
的单调区间.
(![]() )当
)当![]() ,证明:当
,证明:当![]() ,
, ![]() .
.
【答案】(![]() )
)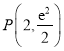 (
(![]() )单调增区间为
)单调增区间为![]() 单调减区间为
单调减区间为![]() (
(![]() )见解析
)见解析
【解析】试题分析:
(1)设点![]() ,根据
,根据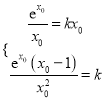 可解得
可解得![]() ,从而可得点
,从而可得点![]() 的坐标.(2)由题意得
的坐标.(2)由题意得![]() ,又
,又![]() ,
, ![]() ,故
,故![]() .从而根据
.从而根据![]() 的符号可得函数的单调区间。(3)结合(2),令
的符号可得函数的单调区间。(3)结合(2),令![]() ,分①
,分①![]() 和②
和②![]() 两种情况都可证得当
两种情况都可证得当![]() 时,
时, ![]() .从而可得
.从而可得![]() ,即不等式成立。
,即不等式成立。
试题解析:
(![]() )设点
)设点![]() ,
,
由![]() ,得
,得![]() ,
,
由题意得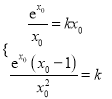 ,解得
,解得![]() ,
,
∴![]() ,
,
∴点![]() 的坐标为
的坐标为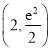 .
.
(![]() )由题意得
)由题意得![]() ,
,
∴![]() ,
,
∵![]() ,
, ![]() ,
,
∴![]() .
.
由![]() ,解得
,解得![]() ,
,
由![]() ,解得
,解得![]() .
.
∴函数![]() 的单调减区间为
的单调减区间为![]() ,单调增区间为
,单调增区间为![]() .
.
(![]() )由(2)得
)由(2)得![]()
设![]() ,则
,则![]() ,
,
由![]() ,得
,得![]() ,
,
①当![]() 时,
时,
则![]() ,
,
∴![]() 在
在![]() 单调递增,
单调递增,
∴![]() ,
,
②当![]() 时,
时,
令![]() ,得
,得![]() ,
,
当![]() 时,
时, ![]() ,
, ![]() 单调递减,
单调递减,
![]() 时,
时, ![]() ,
, ![]() 单调递增。
单调递增。
∴![]() ,
,
综上当![]() 时,
时, ![]() .
.
∴![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增.
单调递增.
∴当![]() 极小值,也为最小值,且
极小值,也为最小值,且![]() 。
。
∴![]() 在
在![]() 成立.
成立.


科目:高中数学 来源: 题型:
【题目】“抛阶砖”是国外游乐场的典型游戏之一.参与者只需将手上的“金币”(设“金币”的半径为1)抛向离身边若干距离的阶砖平面上,抛出的“金币”若恰好落在任何一个阶砖(边长为2.1的正方形)的范围内(不与阶砖相连的线重叠),便可获大奖.不少人被高额奖金所吸引,纷纷参与此游戏,但很少有人得到奖品,请用所学的概率知识解释这是为什么.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对某校高三年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数,根据此数据作出了频数与频率的统计表和频率分布直方图.
分组 | 频数 | 频率 |
[10,15) | 10 | 0.25 |
[15,20) | 24 | n |
[20,25) | m | p |
[25,30] | 2 | 0.05 |
合计 | M | 1 |

(1)求出表中M,p及图中a的值;
(2)若该校高三学生有240人,试估计该校高三学生参加社区服务的次数在区间[10,15)内的人数;
(3)估计这次学生参加社区服务人数的众数、中位数以及平均数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两家外卖公司,其送餐员的日工资方案如下:甲公司的底薪80元,每单抽成4元;乙公司无底薪,40单以内(含40单)的部分每单抽成6元,超出40单的部分每单抽成7元,假设同一公司送餐员一天的送餐单数相同,现从两家公司各随机抽取一名送餐员,并分别记录其50天的送餐单数,得到如下频数表:
甲公司送餐员送餐单数频数表
送餐单数 | 38 | 39 | 40 | 41 | 42 |
天数 | 10 | 15 | 10 | 10 | 5 |
乙公司送餐员送餐单数频数表
送餐单数 | 38 | 39 | 40 | 41 | 42 |
天数 | 5 | 10 | 10 | 20 | 5 |
(1)现从甲公司记录的50天中随机抽取3天,求这3天送餐单数都不小于40的概率;
(2)若将频率视为概率,回答下列两个问题:
①记乙公司送餐员日工资为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望;
的分布列和数学期望;
②小王打算到甲、乙两家公司中的一家应聘送餐员,如果仅从日工资的角度考虑,请利用所学的统计学知识为小王作出选择,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学举行一次“环保知识竞赛”,全校学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为![]() 分)作为样本进行统计,请根据下面尚未完成并有局部污损的样本的频率分布表和频率分布直方图(如图所示)解决下列问题:
分)作为样本进行统计,请根据下面尚未完成并有局部污损的样本的频率分布表和频率分布直方图(如图所示)解决下列问题:
(Ⅰ)写出![]() ,
, ![]() ,
, ![]() ,
, ![]() 的值.
的值.
(Ⅱ)在选取的样本中,从竞赛成绩是![]() 分以上(含
分以上(含![]() 分)的同学中随机抽取
分)的同学中随机抽取![]() 名同学到广场参加环保知识的志愿宣传活动,求所抽取的
名同学到广场参加环保知识的志愿宣传活动,求所抽取的![]() 名同学来自同一组的概率.
名同学来自同一组的概率.
(Ⅲ)在(Ⅱ)的条件下,设![]() 表示所抽取的
表示所抽取的![]() 名同学中来自第
名同学中来自第![]() 组的人数,求
组的人数,求![]() 的分布列及其数学期望.
的分布列及其数学期望.
组别 | 分组 | 频数 | 频率 |
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
合计 |
|
|

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)的最小值为-4,且关于x的不等式f(x)≤0的解集为{x|-1≤x≤3,x∈R}.
(1)求函数f(x)的解析式;
(2)求函数![]() 的零点个数.
的零点个数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com