
【题目】在![]() 中,角
中,角![]() 所对的边分别为
所对的边分别为![]() ,且
,且![]() .
.
(1)求角![]() 的大小;
的大小;
(2)若![]() ,求
,求![]() 周长的最大值.
周长的最大值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)已知等式利用正弦定理化简,由![]() 求出
求出![]() 的值,即可确定出
的值,即可确定出![]() 的度数;(2)由余弦定理列出关系式,得到
的度数;(2)由余弦定理列出关系式,得到![]() ,化简为
,化简为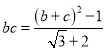 ,用基本不等式可得到
,用基本不等式可得到![]() 的最值,得到周长的最大值.
的最值,得到周长的最大值.
试题解析:(1)![]() ,即为
,即为![]() ,
,
代入正弦定理得:![]() ........................2分
........................2分
又![]() ,
,![]() ,∴
,∴![]() ,即
,即![]() ................4分
................4分
又![]() ,∴
,∴![]() ............6分
............6分
(2)由余弦定理得![]() ,即
,即![]() ,
,
化简得,![]() ,.....................7分
,.....................7分
∵![]() ,∴
,∴![]() ,∴
,∴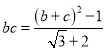 ,.........8分
,.........8分
∵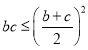 ,∴
,∴ ,当且仅当
,当且仅当![]() 时取等号成立,
时取等号成立,
解得![]() ,
,
∴![]() (当且仅当
(当且仅当![]() 时取等号),.......................11分
时取等号),.......................11分
∴![]() (当且仅当
(当且仅当![]() 时取等号),
时取等号),
∴![]() 周长的最大值为
周长的最大值为![]() .............................12分
.............................12分


科目:高中数学 来源: 题型:
【题目】设函数f(x)=(x﹣a)2lnx,a∈R.
(I)若x=e是y=f(x)的极值点,求实数a的值;
(Ⅱ)若函数y=f(x)﹣4e2只有一个零点,求实数a的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】时下,租车已经成为新一代的流行词,租车自驾游也慢慢流行起来,某小车租车点的收费标准是,不超过2天按照300元计算;超过两天的部分每天收费标准为100元(不足1天的部分按1天计算).有甲乙两人相互独立来该租车点租车自驾游(各租一车一次),设甲、乙不超过2天还车的概率分别为![]() ;2天以上且不超过3天还车的概率分别
;2天以上且不超过3天还车的概率分别![]() ;两人租车时间都不会超过4天.
;两人租车时间都不会超过4天.
(1)求甲所付租车费用大于乙所付租车费用的概率;
(2)设甲、乙两人所付的租车费用之和为随机变量![]() ,求
,求![]() 的分布列与数学期望
的分布列与数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的焦点
的焦点![]() ,过右焦点
,过右焦点![]() 的直线
的直线![]() 与
与![]() 相交于
相交于![]() 两点,若
两点,若![]() 的周长为短轴长的
的周长为短轴长的![]() 倍.
倍.
(1)求![]() 的离心率;
的离心率;
(2)设![]() 的斜率为
的斜率为![]() ,在
,在![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() ?若存在,求出点
?若存在,求出点![]() 的坐标; 若不存在,说明理由.
的坐标; 若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人在如图所示的直角边长为4米的三角形地块的每个格点(指纵、横直线的交叉点以及三角形顶点)处都种了一株相同品种的作物.根据历年的种植经验,一株该种作物的年收获![]() (单位:
(单位:![]() )与它的“相近”作物株数
)与它的“相近”作物株数![]() 之间的关系如下表所示:
之间的关系如下表所示:
| 1 | 2 | 3 | 4 |
| 51 | 48 | 45 | 42 |
这里,两株作物“相近”是指它们之间的直线距离不超过1米.
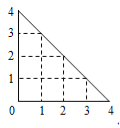
(1)从三角形地块的内部和边界上分别随机选取一株作物,求它们恰好“相近”的概率;
(2)在所种作物中堆积选取一株,求它的年收获量的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法:①将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变;②设有一个回归方程![]() ,变量
,变量![]() 增加一个单位时,
增加一个单位时,![]() 平均增加5个单位;③线性回归方程
平均增加5个单位;③线性回归方程![]() 必过
必过![]() ;④在吸烟与患肺病这两个分类变量的计算中,从独立性检验知,有99%的把握认为吸烟与患肺病有关系时,我们说某人吸烟,那么他有99%的可能患肺病;其中错误的个数是( )
;④在吸烟与患肺病这两个分类变量的计算中,从独立性检验知,有99%的把握认为吸烟与患肺病有关系时,我们说某人吸烟,那么他有99%的可能患肺病;其中错误的个数是( )
A.0 B.1 C. 2 D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】食品安全问题越来越引起人们的重视,农药、化肥的滥用对人民群众的健康带来一定的危害,为了给消费者带来放心的蔬菜,某农村合作社每年投入200万元,搭建了甲、乙两个无公害蔬菜大棚,每个大棚至少要投入20万元,其中甲大棚种西红柿,乙大棚种黄瓜,根据以往的种菜经验,发现种西红柿的年收入![]() 种黄瓜的年收入
种黄瓜的年收入![]() 与投入
与投入![]() (单位:万元)满足
(单位:万元)满足![]() .设甲大棚的投入为
.设甲大棚的投入为![]() (单位:万元),每年两个大棚的总收益为
(单位:万元),每年两个大棚的总收益为![]() (单位:万元)
(单位:万元)
(1)求![]() 的值;
的值;
(2)试问如何安排甲、乙两个大棚的投入,才能使总收益![]() 最大?
最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中石化集团获得了某地深海油田区块的开采权,集团在该地区随机初步勘探了部分儿口井,取得了地质资料.进入全面勘探时期后,集团按网络点来布置井位进行全面勘探. 由于勘探一口井的费用很高,如果新设计的井位与原有井位重合或接近,便利用旧井的地质资料,不必打这口新井,以节约勘探费用.勘探初期数据资料见如表:

(Ⅰ)1~6号旧井位置线性分布,借助前5组数据求得回归直线方程为![]() ,求
,求![]() ,并估计
,并估计![]() 的预报值;
的预报值;
(Ⅱ)现准备勘探新井![]() ,若通过1、3、5、7号井计算出的
,若通过1、3、5、7号井计算出的![]() 的值(
的值(![]() 精确到0.01)相比于(Ⅰ)中
精确到0.01)相比于(Ⅰ)中![]() 的值之差不超过10%,则使用位置最接近的已有旧井
的值之差不超过10%,则使用位置最接近的已有旧井![]() ,否则在新位置打开,请判断可否使用旧井?
,否则在新位置打开,请判断可否使用旧井?
(参考公式和计算结果: )
)
(Ⅲ)设出油量与勘探深度的比值![]() 不低于20的勘探并称为优质井,那么在原有井号1~6的出油量不低于50L的井中任意勘探3口井,求恰好2口是优质井的概率.
不低于20的勘探并称为优质井,那么在原有井号1~6的出油量不低于50L的井中任意勘探3口井,求恰好2口是优质井的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com