
分析 (Ⅰ)由条件,将n换为n-1,两式相减,求出a2=3,再由等比数列的通项公式,即可得到所求;
(Ⅱ)bn=log3an+1=log33n=n,运用等差数列的求和公式可得Tn,再由$\frac{1}{{T}_{n}}$=$\frac{2}{n(n+1)}$=2($\frac{1}{n}$-$\frac{1}{n+1}$),运用分组求和裂项相消求和,化简即可得到所求和.
解答 解:(Ⅰ)a1=1,2Sn=an+1-1,
可得2Sn-1=an-1,(n≥2),
两式相减可得,2an=2Sn-2Sn-1=an+1-an,
即有an+1=3an(n≥2),
由2a1=2S1=a2-1,可得a2=3,
则an=a2qn-2=3•3n-2=3n-1,对n=1也成立,
则{an}的通项公式为an=3n-1;
(Ⅱ)bn=log3an+1=log33n=n,
则前n项和为Tn=$\frac{1}{2}$n(n+1),
可得$\frac{1}{{T}_{n}}$=$\frac{2}{n(n+1)}$=2($\frac{1}{n}$-$\frac{1}{n+1}$),
则数列{$\frac{1}{{T}_{n}}$}的前n项和为2(1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{n}$-$\frac{1}{n+1}$)
=2(1-$\frac{1}{n+1}$)=$\frac{2n}{n+1}$;
数列{4an}的前n项和为4•$\frac{1-{3}^{n}}{1-3}$=2(3n-1).
则数列{$\frac{1}{{T}_{n}}$+4an}的前n项和为$\frac{2n}{n+1}$+2(3n-1).
点评 本题考查数列的通项公式的求法,注意运用数列递推式,考查数列的求和方法:直接法和裂项相消求和,考查化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | 3 | C. | $3\sqrt{2}$ | D. | -3或3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{π}{6}$,-1) | B. | ($\frac{π}{3}$,-1) | C. | ($\frac{π}{6}$,0) | D. | ($\frac{π}{3}$,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{7}$,$\frac{1}{5}$]∪{3} | B. | [3,5]∪{$\frac{1}{7}$} | C. | [$\frac{1}{7}$,$\frac{1}{3}$)∪{5} | D. | [3,7)∪{$\frac{1}{5}$} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
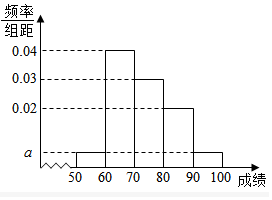 某小学1000名学生期中考试数学成绩的频率分布直方图如图所示.其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].根据统计学的知识估计成绩在[80,90)内的人数约为200.
某小学1000名学生期中考试数学成绩的频率分布直方图如图所示.其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].根据统计学的知识估计成绩在[80,90)内的人数约为200.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 进位制是人们为了计数和运算方便而约定的记数系统,在日常生活中,我们最熟悉、最常用的是十进制.如图是实现将某进制数a化为十进制数b的程序框图,若输入的k=2,a=110,n=3,则输出的b=( )
进位制是人们为了计数和运算方便而约定的记数系统,在日常生活中,我们最熟悉、最常用的是十进制.如图是实现将某进制数a化为十进制数b的程序框图,若输入的k=2,a=110,n=3,则输出的b=( )| A. | 14 | B. | 12 | C. | 6 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com