
| 身高x(cm) | 155 | 161 | a | 167 | 174 |
| 体重y(kg) | 49 | 53 | 56 | 58 | 64 |
分析 根据表中数据计算$\overline{y}$,由回归直线经过样本中心($\overline{x}$,$\overline{y}$),求出$\overline{x}$的值,再由平均数的概念求出a的值.
解答 解:由表中数据计算$\overline{y}$=$\frac{1}{5}$×(49+53+56+58+64)=56,
根据回归直线经过样本中心($\overline{x}$,$\overline{y}$),
可得56=0.79$\overline{x}$-73.56,
解得$\overline{x}$=164;
由$\overline{x}$=$\frac{1}{5}$×(155+161+a+157+174)=164,
解得a=163,
故答案为:163.
点评 本题主要考查了线性回归方程过样本中心点的应用问题,是基础题.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{4+5\sqrt{3}}{4}$ | B. | $\frac{8+5\sqrt{3}}{4}$ | C. | 3 | D. | $\frac{4+\sqrt{5}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | $\frac{1}{5}$ | C. | $\frac{11}{2}$ | D. | $\frac{2}{11}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=log${\;}_{\frac{1}{2}}$|x| | B. | y=x${\;}^{\frac{1}{2}}$ | C. | y=$\frac{{{2^x}+{2^{-x}}}}{2}$ | D. | y=lg$\frac{2-x}{2+x}$ |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年浙江普通高校招生学业水平考试数学试卷(解析版) 题型:选择题
设函数 ,
,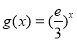 ,其中
,其中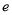 为自然对数的底数,则( )
为自然对数的底数,则( )
A.对于任意实数 恒有
恒有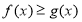
B.存在正实数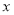 使得
使得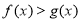
C.对于任意实数 恒有
恒有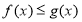
D.存在正实数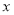 使得
使得
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com