Question

【题目】如图所示，该几何体是由一个直三棱柱ADE﹣BCF和一个正四棱锥P﹣ABCD组合而成，AD⊥AF，AE=AD=2．
（Ⅰ）证明：平面PAD⊥平面ABFE；
（Ⅱ）求正四棱锥P﹣ABCD的高h，使得二面角C﹣AF﹣P的余弦值是 ．

Answer 1

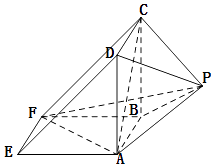
【答案】证明：（Ⅰ）∵几何体是由一个直三棱柱ADE﹣BCF和一个正四棱锥P﹣ABCD组合而成， ∴AD⊥AF，AD⊥AB，
又AF∩AB=A，
∴AD⊥平面ABEF，
又AD平面PAD，
∴平面PAD⊥平面ABFE．
解：（Ⅱ）以A 为原点，AB、AE、AD的正方向为x，y，z轴，建立空间直角坐标系A﹣xyz
设正四棱棱的高为h，AE=AD=2，
则A（0，0，0），F（2，2，0），C（2，0，2），P（1，﹣1，1）
设平面ACF的一个法向量 =（x，y，z），
=（2，2，0）， =（2，0，2），
则 ，取x=1，得 =（1，﹣1，﹣1），
设平面ACP的一个法向量 =（a，b，c），
则 ，取b=1，则 =（﹣1，1，1+h），
二面角C﹣AF﹣P的余弦值 ，
∴|cos＜ ＞|= = = ，
解得h=1．

【解析】（Ⅰ）推导出AD⊥AF，AD⊥AB，从而AD⊥平面ABEF，由此能证明平面PAD⊥平面ABFE．（Ⅱ）以A 为原点，AB、AE、AD的正方向为x，y，z轴，建立空间直角坐标系A﹣xyz，利用向量法能求出h的值．